题目内容
 如图所示,已知三棱柱A′B′C′-ABC的侧棱垂直于底面,AC⊥CB,且AC=CB=CC′=2.若点E为A′B′中点,则CE与底面ABC所成角的余弦值为
如图所示,已知三棱柱A′B′C′-ABC的侧棱垂直于底面,AC⊥CB,且AC=CB=CC′=2.若点E为A′B′中点,则CE与底面ABC所成角的余弦值为
| ||
| 3 |
| ||
| 3 |
分析:利用线面所成角的定义先确定线面所成的角然后求出线面所成的角即可.
解答:解:过E做EF⊥AB于F,则F为AB的中点.
连结CF,则∠ECF为CE与底面ABC所成的角.
所以CF=
,EF=2,所以CE=
,
所以cos∠ECF=
=
=
.
故答案为:
.

连结CF,则∠ECF为CE与底面ABC所成的角.
所以CF=
| 2 |
| 6 |
所以cos∠ECF=
| CF |
| CE |
| ||
|
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题主要考查空间直线和平面所成角的求法,先找出线面角,然后根据边角关系求出即可.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 如图所示,已知三棱柱ABC-A1B1C1的各棱长均为2,侧棱B1B与底面ABC所成的角为,且侧面ABB1A1垂直于底面ABC.
如图所示,已知三棱柱ABC-A1B1C1的各棱长均为2,侧棱B1B与底面ABC所成的角为,且侧面ABB1A1垂直于底面ABC. 如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1-ABC1的体积为( )
如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1-ABC1的体积为( ) 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 上的
上的 的中点,则异面直线
的中点,则异面直线 与
与 所成的角的余弦值为( )
所成的角的余弦值为( ) B.
B.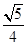 C.
C. D.
D.

 ,在某个空间直角坐标系中,
,在某个空间直角坐标系中, ,
, ,其中
,其中 、
、

 ,求直线
,求直线 与平面
与平面 所成角的大小。
所成角的大小。