题目内容
 如图所示,已知三棱柱ABC-A1B1C1的各棱长均为2,侧棱B1B与底面ABC所成的角为,且侧面ABB1A1垂直于底面ABC.
如图所示,已知三棱柱ABC-A1B1C1的各棱长均为2,侧棱B1B与底面ABC所成的角为,且侧面ABB1A1垂直于底面ABC.(1)证明AB⊥CB1;?
(2)求三棱锥B1-ABC的体积;?
(3)求二面角C-AB1-B的大小.
分析:(1)在平面ABB1A1内,过B1作B1D⊥AB于D,由侧面ABB1A1⊥平面ABC,知B1D⊥平面ABC,故∠B1BA是B1B与底面ABC所成的角,由此能够证明AB⊥CB1.
(2)由B1D⊥平面ABC,知B1D是三棱锥B1-ABC的高,由B1B=2,∠B1BA=60°,得B1D=2sin60°=
.由此能求出三棱锥B1-ABC的体积.
(3)由△ABC是正三角形,CD⊥AB,CD⊥B1D,知CD⊥平面ABB1.在平面ABB1中作DE⊥AB1于E,连接CE,则CE⊥AB1,故∠CED为二面角C-AB1-B的平面角,由此能求出二面角C-AB1-B的大小.
(2)由B1D⊥平面ABC,知B1D是三棱锥B1-ABC的高,由B1B=2,∠B1BA=60°,得B1D=2sin60°=
| 3 |
(3)由△ABC是正三角形,CD⊥AB,CD⊥B1D,知CD⊥平面ABB1.在平面ABB1中作DE⊥AB1于E,连接CE,则CE⊥AB1,故∠CED为二面角C-AB1-B的平面角,由此能求出二面角C-AB1-B的大小.
解答:解:(1)在平面ABB1A1内,过B1作B1D⊥AB于D,
∵侧面ABB1A1⊥平面ABC,∴B1D⊥平面ABC,
∴∠B1BA是B1B与底面ABC所成的角,
∴∠B1BA=60°,(2分)
∵三棱柱的各棱长均为2.
∴△ABB1是正三角形,
∴D是AB的中点,连接CD.
在正△ABC中,CD⊥AB,
∴AB⊥CB1.(4分)
(2)∵B1D⊥平面ABC,
∴B1D是三棱锥B1-ABC的高,
∴由B1B=2,∠B1BA=60°,
得B1D=2sin60°=
.(6分)
∴VE1-ABC=
S△ABC•B1D
=
(
×
×2×2)•
=1.(8分)
(3)∵△ABC是正三角形,CD⊥AB,CD⊥B1D,
∴CD⊥平面ABB1.
在平面ABB1中作DE⊥AB1于E,连接CE,则CE⊥AB1,
∴∠CED为二面角C-AB1-B的平面角,(10分)
在Rt△CED中,CD=2sin60°=
,
连接BA1交AB1于O,则BO=
,
∴DE=
BO=
,∴tanCED=
=2,
∴所求二面角C-AB1-B的大小为arctan2.(12分)
∵侧面ABB1A1⊥平面ABC,∴B1D⊥平面ABC,
∴∠B1BA是B1B与底面ABC所成的角,
∴∠B1BA=60°,(2分)
∵三棱柱的各棱长均为2.
∴△ABB1是正三角形,
∴D是AB的中点,连接CD.
在正△ABC中,CD⊥AB,
∴AB⊥CB1.(4分)
(2)∵B1D⊥平面ABC,
∴B1D是三棱锥B1-ABC的高,
∴由B1B=2,∠B1BA=60°,
得B1D=2sin60°=
| 3 |
∴VE1-ABC=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
(3)∵△ABC是正三角形,CD⊥AB,CD⊥B1D,
∴CD⊥平面ABB1.
在平面ABB1中作DE⊥AB1于E,连接CE,则CE⊥AB1,
∴∠CED为二面角C-AB1-B的平面角,(10分)
在Rt△CED中,CD=2sin60°=
| 3 |
连接BA1交AB1于O,则BO=
| 3 |
∴DE=
| 1 |
| 2 |
| ||
| 2 |
| CD |
| DE |
∴所求二面角C-AB1-B的大小为arctan2.(12分)
点评:本题考查异面直线垂直的证明,考查三棱锥体积的求法,考查二面角的大小的求法.解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,已知三棱柱A′B′C′-ABC的侧棱垂直于底面,AC⊥CB,且AC=CB=CC′=2.若点E为A′B′中点,则CE与底面ABC所成角的余弦值为
如图所示,已知三棱柱A′B′C′-ABC的侧棱垂直于底面,AC⊥CB,且AC=CB=CC′=2.若点E为A′B′中点,则CE与底面ABC所成角的余弦值为 如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1-ABC1的体积为( )
如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1-ABC1的体积为( ) 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 上的
上的 的中点,则异面直线
的中点,则异面直线 与
与 所成的角的余弦值为( )
所成的角的余弦值为( ) B.
B.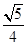 C.
C. D.
D.

 ,在某个空间直角坐标系中,
,在某个空间直角坐标系中, ,
, ,其中
,其中 、
、

 ,求直线
,求直线 与平面
与平面 所成角的大小。
所成角的大小。