题目内容
已知椭圆 :
: (
( )过点
)过点 ,其左、右焦点分别为
,其左、右焦点分别为 ,且
,且 .
.
(1)求椭圆 的方程;
的方程;
(2)若 是直线
是直线 上的两个动点,且
上的两个动点,且 ,则以
,则以 为直径的圆
为直径的圆 是否过定点?请说明理由.
是否过定点?请说明理由.
【答案】
(1)  (2) 圆必过定点
(2) 圆必过定点 和
和
【解析】
试题分析:(1)设点 的坐标分别为
的坐标分别为 ,则
,则 ,故
,故 ,可得
,可得 ,
,
所以 ,
, ,
,
∴ ,所以椭圆
,所以椭圆 的方程为
的方程为 .
.
(2)设 的坐标分别为
的坐标分别为 ,则
,则 ,
, . 由
. 由 ,可得
,可得 ,即
,即 ,
,
又圆 的圆心为
的圆心为 半径为
半径为 ,故圆
,故圆 的方程为
的方程为 ,即
,即 ,也就是
,也就是 ,令
,令 ,可得
,可得 或
或 ,
,
故圆 必过定点
必过定点 和
和 .
.
考点:椭圆与圆的方程及性质
点评:第一小题利用向量的坐标运算及椭圆定义可求得方程;第二小题判定曲线是否过定点只需看曲线方程中能否转化出与参数无关的关系式

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (
( )过点
)过点 (0,2),离心率
(0,2),离心率 .
. (2,0)的直线
(2,0)的直线 与椭圆相交于
与椭圆相交于 两点,且
两点,且 为锐角(其中
为锐角(其中 为坐标原点),求直线
为坐标原点),求直线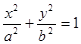 (
(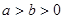 )过点
)过点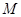 (0,2),离心率
(0,2),离心率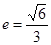 .
.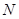 (2,0)的直线
(2,0)的直线 与椭圆相交于
与椭圆相交于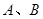 两点,且
两点,且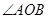 为锐角(其中
为锐角(其中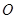 为坐标原点),求直线
为坐标原点),求直线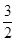 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。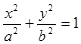 (
(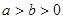 )过点
)过点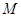 (0,2),离心率
(0,2),离心率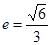 .
.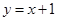 与椭圆相交于
与椭圆相交于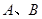 两点,求
两点,求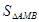 .
. 过点
过点 ,且长轴长等于4.
,且长轴长等于4.  是椭圆C的两个焦点,⊙O是以
是椭圆C的两个焦点,⊙O是以 为直径的圆,直线
为直径的圆,直线 与⊙O相切,并与椭圆C交于不同的两点A、B,若
与⊙O相切,并与椭圆C交于不同的两点A、B,若 ,求
,求 的值.
的值.