题目内容
已知椭圆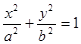 (
(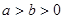 )过点
)过点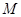 (0,2),离心率
(0,2),离心率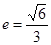 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过定点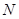 (2,0)的直线
(2,0)的直线 与椭圆相交于
与椭圆相交于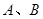 两点,且
两点,且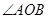 为锐角(其中
为锐角(其中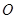 为坐标原点),求直线
为坐标原点),求直线 斜率的取值范围.
斜率的取值范围.
【答案】
(Ⅰ) (Ⅱ)
(Ⅱ)
【解析】
试题分析:(Ⅰ)由题意得
结合 ,解得
,解得
所以,椭圆的方程为 .
.
(Ⅱ)
设 ,则
,则 .
.
设直线 的方程为:
的方程为: 由
由 得
得
即 .
.
所以 ,
,





解得 .
.
故. 为所求.
为所求.
考点:椭圆方程性质及椭圆与直线的位置关系
点评:有关于椭圆与直线相交问题,将椭圆方程与直线方程联立方程组,利用韦达定理计算是常用的转化思路,平面解析几何中涉及到的向量通常用向量的坐标运算来化简,本题中 为锐角转化为向量夹角是锐角,进而用向量的数量积来表示
为锐角转化为向量夹角是锐角,进而用向量的数量积来表示

练习册系列答案
相关题目
 (
( )过点
)过点 (0,2),离心率
(0,2),离心率 .
. (2,0)的直线
(2,0)的直线 与椭圆相交于
与椭圆相交于 两点,且
两点,且 为锐角(其中
为锐角(其中 为坐标原点),求直线
为坐标原点),求直线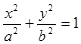 (
(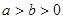 )过点
)过点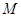 (0,2),离心率
(0,2),离心率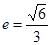 .
.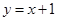 与椭圆相交于
与椭圆相交于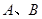 两点,求
两点,求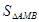 .
.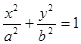 (
( )过点
)过点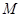 (0,2),离心率
(0,2),离心率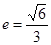 .
. (2,0)的直线
(2,0)的直线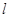 与椭圆相交于
与椭圆相交于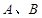 两点,且
两点,且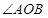 为锐角(其中
为锐角(其中 为坐标原点),求直线
为坐标原点),求直线