Question

（本小题满分12分）已知函数是偶函数.

（1）求k的值；

（2）若方程有解，求m的取值范围.

 

Answer 1

【答案】

（1）k=-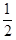

（2）m的取值范围为m≥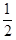

【解析】解：（1）由f(x)是偶函数，则f(1)-f(-1)=0，

?     即log₄(4+1)+k=log₄(4^-1+1)-k，

得k=-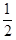.…………………………………………………………………………………… 2分

此时，f(x)=log₄(4^x+1)- 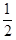x，

f (-x)=log₄(4^-x+1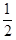）+x=log₄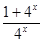+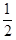x=log₄(4^x+1)- 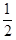x=f(x)

即f(x)为偶函数.…………………………………………………………………………6分

或由于函数f(x)是偶函数，得f(-x)=f(x)，

?      即log₄(4^-x+1)-kx=log₄(4^x+1)+kx  ……………………………………………………………… 2分

∴log₄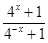=-2kx，∴log₄4^x=-2kx，∴ x=-2kx对一切x恒成立.

∴k=-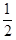.……………………………………………………………………………………6分

（2）由f(x)=log₄(4^x+1)- 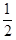x=log₄=log₄(2^x+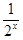）………………………………8分

∵2^x+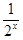≥2,∴ f(x)≥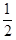.………………………………………………………………10分

∴ m≥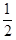

∴ 要使方程f(x)-m=0有解，m的取值范围为m≥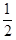………………………………12分