题目内容
(本小题满分12分)
已知函数 的导函数
的导函数 ,数列
,数列 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的图象上.
的图象上.
(Ⅰ)求数列 的通项公式及
的通项公式及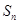 的最大值;
的最大值;
(Ⅱ)令 ,其中
,其中 ,求
,求 的前
的前 项和.
项和.
【答案】
(1)当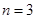 或
或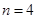 时,
时, 取得最大值
取得最大值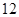
(2)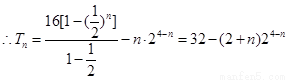
【解析】解:(Ⅰ)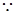
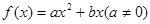 ,
,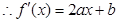
由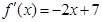 得:
得: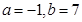 ,所以
,所以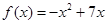 -----------------------2分
-----------------------2分
又因为点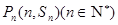 均在函数
均在函数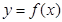 的图象上,所以有
的图象上,所以有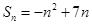
当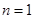 时,
时,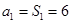
当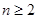 时,
时, ,
,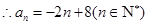 -----------------------4分
-----------------------4分
令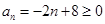 得
得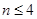 ,
,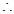 当
当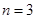 或
或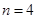 时,
时, 取得最大值
取得最大值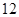
综上, 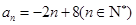 ,当
,当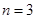 或
或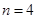 时,
时, 取得最大值
取得最大值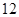 -----------------6分
-----------------6分
(Ⅱ)由题意得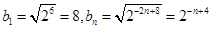 -----------------------8分
-----------------------8分
所以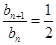 ,即数列
,即数列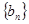 是首项为
是首项为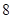 ,公比是
,公比是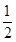 的等比数列
的等比数列
故 的前
的前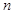 项和
项和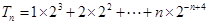 ………………①
………………①
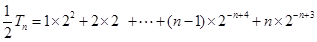 …………②
…………②
所以①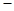 ②得:
②得: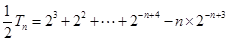 ----------------------10分
----------------------10分
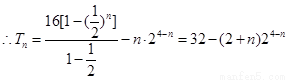 ------------------------12分
------------------------12分

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目