题目内容
曲线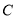 是平面内到直线
是平面内到直线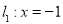 和直线
和直线 的距离之积等于常数
的距离之积等于常数 的点的轨迹,设曲线
的点的轨迹,设曲线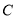 的轨迹方程
的轨迹方程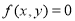 .
.
(1)求曲线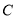 的方程
的方程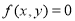 ;
;
(2)定义:若存在圆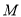 使得曲线
使得曲线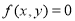 上的每一点都落在圆
上的每一点都落在圆 外或圆
外或圆 上,则称圆
上,则称圆 为曲线
为曲线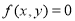 的收敛圆.判断曲线
的收敛圆.判断曲线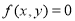 是否存在收敛圆?若存在,求出收敛圆方程;若不存在,请说明理由.
是否存在收敛圆?若存在,求出收敛圆方程;若不存在,请说明理由.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)设出点 ,利用直接法求轨迹方程;(2)根据题中所给定义进行验证求解.
,利用直接法求轨迹方程;(2)根据题中所给定义进行验证求解.
试题解析:(1)设动点为 ,则由条件可知轨迹方程是
,则由条件可知轨迹方程是 ; 3分
; 3分
(2)设 为曲线
为曲线 上任意一点,可以证明
上任意一点,可以证明
则点 关于直线
关于直线 、点
、点 及直线
及直线 对称的点仍在曲线
对称的点仍在曲线 上 6分
上 6分
根据曲线 的对称性和圆的对称性,若存在收敛圆,
的对称性和圆的对称性,若存在收敛圆,
则该收敛圆的方程是 7分
7分
讨论: 时
时 最多一个有一个交点
最多一个有一个交点 满足条件 8分
满足条件 8分
(1)代入(2)得 10分
10分
曲线 存在收敛圆 11分
存在收敛圆 11分
收敛圆的方程是 .
.
考点:1.动点的轨迹方程;2.新定义型题目;3.点与圆的位置关系.
考点分析: 考点1:直线和圆的位置关系 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
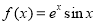
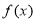 的单调区间;
的单调区间; 时,
时,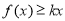 ,求实数
,求实数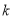 的取值范围
的取值范围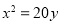 的焦点重合,且其渐近线的方程为
的焦点重合,且其渐近线的方程为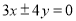 ,则该双曲线的标准方程为( )
,则该双曲线的标准方程为( )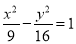 B.
B.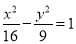 C.
C.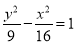 D.
D.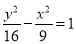
 是分别经过
是分别经过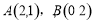 两点的两条平行直线,当
两点的两条平行直线,当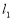 的方程是 .
的方程是 . 满足
满足 (
( 为虚数单位),则复数
为虚数单位),则复数 .
.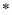 ”:
”: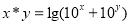 ,
,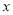 、
、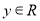 。对于任意实数
。对于任意实数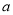 、
、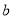 、
、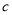 ,给出如下结论:①
,给出如下结论:①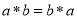 ;②
;②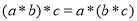 ;③
;③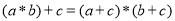 .其中正确结论的个数是 ( )
.其中正确结论的个数是 ( )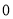 个 B.
个 B.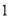 个 C.
个 C.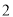 个 D.
个 D.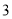 个
个 、
、 是不同的直线,
是不同的直线, 、
、 是不同的平面,且
是不同的平面,且 ,
, ,则下列命题正确的是( )
,则下列命题正确的是( ) ,则
,则
 ,则
,则
 ,
, 对任意的实数x成立,则称f(x)是回旋函数.
对任意的实数x成立,则称f(x)是回旋函数. 为回旋函数,则t>l;
为回旋函数,则t>l; 不是回旋函数;
不是回旋函数; :
: 经过点
经过点 ,则直线
,则直线 在
在 轴和
轴和 轴的截距之和的最
轴的截距之和的最