题目内容
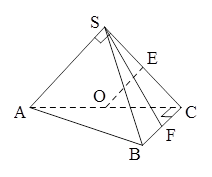
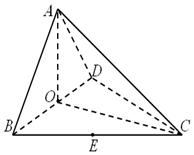
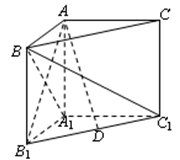
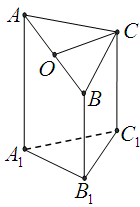
如图,在三棱锥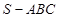 中,侧面
中,侧面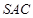 与底面
与底面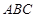 垂直,
垂直, 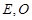 分别是
分别是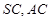 的中点,
的中点,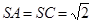 ,
,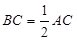 ,
,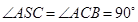 .
.
(Ⅰ)求证: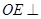 平面
平面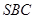 ;
;
(Ⅱ)若点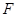 为线段
为线段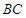 的中点,求异面直线
的中点,求异面直线 与
与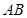 所成角的正切值.
所成角的正切值.
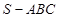 中,侧面
中,侧面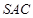 与底面
与底面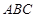 垂直,
垂直, 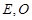 分别是
分别是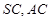 的中点,
的中点,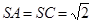 ,
,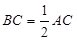 ,
,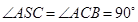 .
.
(Ⅰ)求证:
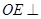 平面
平面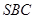 ;
;(Ⅱ)若点
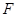 为线段
为线段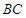 的中点,求异面直线
的中点,求异面直线 与
与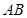 所成角的正切值.
所成角的正切值. (1)详见解析;(2)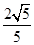
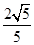
试题分析:(Ⅰ)因为
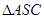 中,
中,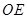 是中位线,故
是中位线,故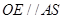 ,所以要证明
,所以要证明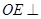 平面
平面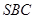 ,只需证明
,只需证明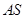
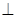 平面
平面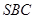 ,因为
,因为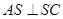 ,故只需证明
,故只需证明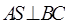 ,由已知侧面
,由已知侧面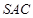 与底面
与底面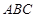 垂直且
垂直且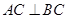 ,故
,故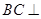 面
面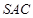 ,从而
,从而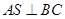 ,进而证明
,进而证明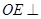 平面
平面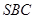 ;(Ⅱ)连接
;(Ⅱ)连接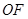 ,因为
,因为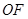 是
是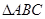 的中位线,则
的中位线,则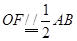 ,则
,则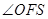 就是异面直线
就是异面直线 与
与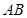 所成的角,连接
所成的角,连接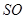 ,由已知得
,由已知得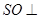 面
面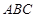 ,则
,则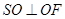 ,在
,在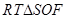 中求
中求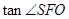 即可.
即可.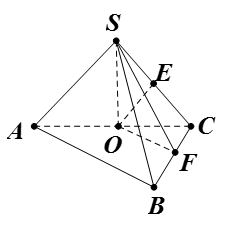
试题解析:(Ⅰ)

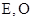 分别是
分别是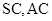 的中点
的中点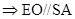
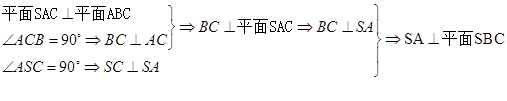
由①②知
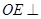 平面
平面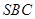 .
.(Ⅱ)连接
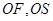 ,
,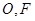 是
是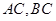 的中点
的中点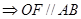 且
且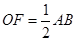
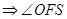 是异面直线
是异面直线 与
与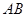 所成的角.
所成的角.等腰直角三角形
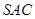 中
中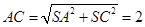 ,且
,且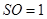 ,
,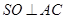
又平面
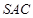
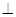 平面
平面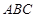 ,所以
,所以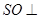 平面
平面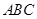 ,
,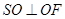 ,
,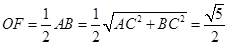 . ,
. ,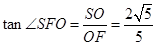 .
.
练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
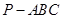 中,
中,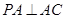 ,
,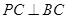 ,
,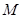 为
为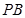 的中点,
的中点,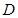 为
为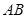 的中点,且
的中点,且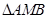 为正三角形.
为正三角形.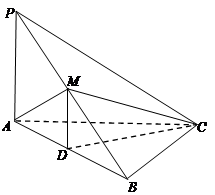
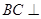 平面
平面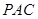 ;
;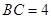 ,
,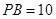 ,求点
,求点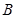 到平面
到平面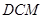 的距离.
的距离. 中,
中,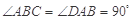 ,
,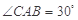 ,
,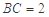 ,
,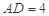 . 把
. 把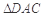 沿对角线
沿对角线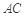 折起到
折起到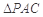 的位置,如图2所示,使得点
的位置,如图2所示,使得点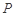 在平面
在平面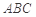 上的正投影
上的正投影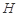 恰好落在线段
恰好落在线段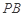 ,点
,点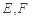 分别为线段
分别为线段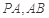 的中点.
的中点. 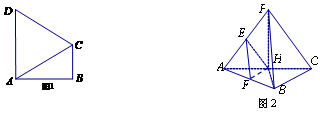
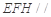 平面
平面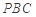 ;
;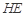 与平面
与平面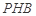 所成角的正弦值;
所成角的正弦值;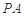 上是否存在一点
上是否存在一点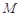 ,使得
,使得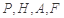 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.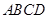 中,
中,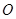 、
、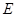 分别是
分别是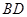 、
、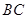 的中点,
的中点,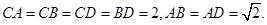
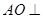 平面
平面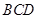 ;
;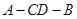 的正切值;
的正切值;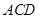 的距离.
的距离.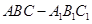 中,
中,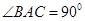 ,
,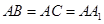 .
.
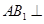 平面
平面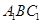 ;
;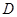 为
为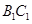 的中点,求
的中点,求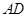 与平面
与平面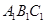 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为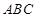 .已知
.已知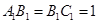 ,
,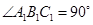 ,
,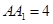 ,
,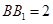 ,
,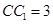 .
.
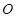 是
是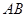 的中点,证明:
的中点,证明: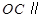 平面
平面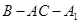 的大小;
的大小;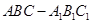 中,
中,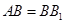 ,
,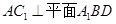 ,
,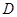 为的
为的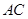 中点.
中点.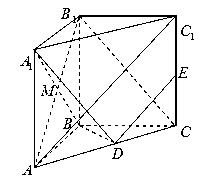
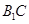 ∥平面
∥平面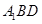 ;
;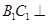 平面
平面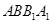 ;
;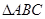 中,
中,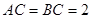 ,
,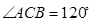 ,
,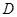 为
为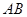 的中点,
的中点,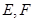 分别在线段
分别在线段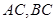 上的动点,且
上的动点,且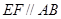 ,
,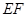 交
交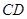 于
于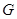 ,把
,把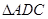 沿
沿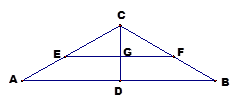
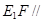 平面
平面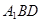 ;
;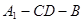 为直二面角时,是否存在点
为直二面角时,是否存在点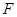 ,使得直线
,使得直线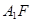 与平面
与平面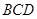 所成的角为
所成的角为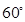 ,若存在求
,若存在求 的长,若不存在说明理由。
的长,若不存在说明理由。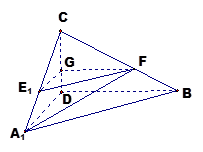
 为直线,
为直线,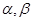 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )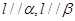 ,则
,则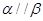
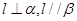 ,则
,则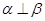
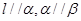 ,则
,则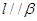
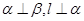 ,则
,则