题目内容
已知函数 ,
,
(1)判断函数的单调性,并用定义证明;
(2)求函数的最大值和最小值.
(1)解:f(x)在[3,5]上为增函数.证明如下:…(2分)
设x1,x2是区间[3,5]上的任意两个实数且x1<x2,
则 …(4分)
…(4分)
∵3≤x1<x2≤5∴2-x1<0,2-x2<0 x1-x2<0
∴f(x1)-f(x2)<0 即f(x1)<f(x2)
∴f(x)在[3,5]上为增函数…(8分)
(2)由(1)f(x)在[3,5]上为增函数,
所以f(x)在[3,5]上有最大值f(5)=-2,有最小值f(3)=-4…(12分)
分析:(1)任取3≤x1<x2≤5,我们构造出f(x2)-f(x1)的表达式,根据实数的性质,我们易出f(x2)-f(x1)的符号,进而根据函数单调性的定义,得到答案;
(2)根据(1)可知函数的单调性,将区间端点的值代入即可求出最大值和最小值.
点评:本题主要考查函数单调性的判断与证明,以及应用单调性求函数的最值,同时还考查了学生的变形,转化能力,属中档题.
设x1,x2是区间[3,5]上的任意两个实数且x1<x2,
则
 …(4分)
…(4分)∵3≤x1<x2≤5∴2-x1<0,2-x2<0 x1-x2<0
∴f(x1)-f(x2)<0 即f(x1)<f(x2)
∴f(x)在[3,5]上为增函数…(8分)
(2)由(1)f(x)在[3,5]上为增函数,
所以f(x)在[3,5]上有最大值f(5)=-2,有最小值f(3)=-4…(12分)
分析:(1)任取3≤x1<x2≤5,我们构造出f(x2)-f(x1)的表达式,根据实数的性质,我们易出f(x2)-f(x1)的符号,进而根据函数单调性的定义,得到答案;
(2)根据(1)可知函数的单调性,将区间端点的值代入即可求出最大值和最小值.
点评:本题主要考查函数单调性的判断与证明,以及应用单调性求函数的最值,同时还考查了学生的变形,转化能力,属中档题.

练习册系列答案
相关题目

 ,
, 上的单调性;
上的单调性; .
. ,求a,b的值.
,求a,b的值. .
. 的奇偶性;(4分)
的奇偶性;(4分) 的方程
的方程 有两解,求实数
有两解,求实数 的取值范围;(6分)
的取值范围;(6分) ,记
,记 ,试求函数
,试求函数 在区间
在区间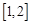 上的最大值.(10分)
上的最大值.(10分) .
. ,
, 的奇偶性;(2)求证:方程
的奇偶性;(2)求证:方程 至少有一根在区间
至少有一根在区间