题目内容
如图,梯形ABCD是等腰梯形,AD∥BC,求证:A、B、C、D共圆.
图2-2-5
答案：
解析：
解析：
|
证明:∵梯形ABCD是等腰梯形,
∴∠A=∠D. 又∵AD∥BC, ∴∠C+∠D=180°. ∴∠A+∠C=180°.∴A、B、C、D共圆. |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
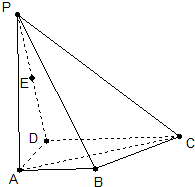如图，ABCD是梯形，AB∥CD，∠BAD=90°，PA⊥面ABCD，且AB=1，AD=1，CD=2，PA=3，E为PD的中点
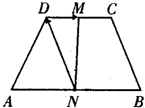如图，ABCD是一个梯形，AB∥CD，且AB=2CD，M、N分别是DC、AB的中点，已知
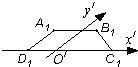如图梯形A1B1C1D1是一平面图形ABCD的斜二侧直观图，若A1D1∥O′y′A1B1∥C1D1，A1B1=