题目内容
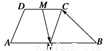
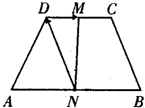如图，ABCD是一个梯形，AB∥CD，且AB=2CD，M、N分别是DC、AB的中点，已知| AB |
| a |
| AD |
| b |
| a |
| b |
| DC |
| BC |
| MN |
分析：根据梯形ABCD的下底等于上底的2倍，得
=
=
．由向量的加法法则，得化简得
=
+
+
=-
+
，同理结合M、N分别是DC、AB的中点算出
=
-
．
| DC |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| a |
| BC |
| BA |
| AD |
| DC |
| 1 |
| 2 |
| a |
| b |
| MN |
| 1 |
| 4 |
| a |
| b |
解答：解：∵AB∥CD，且AB=2CD
∴
=
=
因此，
=
+
+
=-
+
+
=-
+
∵M、N分别是DC、AB的中点，
∴
=
+
+
=-
-
+
=
-
∴
| DC |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| a |
因此，
| BC |
| BA |
| AD |
| DC |
| a |
| b |
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| a |
| b |
∵M、N分别是DC、AB的中点，
∴
| MN |
| MD |
| DA |
| AN |
| 1 |
| 4 |
| a |
| b |
| 1 |
| 2 |
| a |
| 1 |
| 4 |
| a |
| b |
点评：本题在梯形中给出上、下底的中点，求向量的线性表示式．着重考查了梯形的性质、平面向量加减法的运算法则和平面向量的基本定理等知识，属于基础题．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
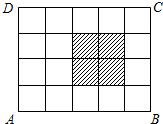
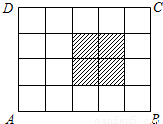
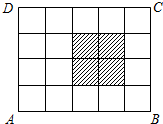如图，ABCD是一个4×5的方格纸，向此四边形ABCD内抛撒一粒豆子，则豆子恰好落在阴影部分内的概率为
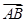＝a，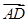
＝b，试用a、b表示
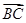和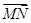
.
