题目内容
（本大题12分）
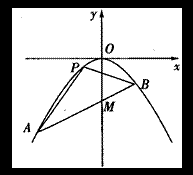如图，抛物线的项点O在坐标原点，焦点在y轴负半轴上，过点M（0，-2）作直线
与抛物线相交于A，B两点，且满足
（I）求直线和抛物线的方程；
（II）当抛物线上一动点P从点A向点B运动时，求
面积的最大值。
(Ⅰ) 直线
的方程为
，抛物线的方程为
(Ⅱ) 
解析:
（I）据题意可设直线的方程为
抛物线的方程为
（2分）
由
（3分），设点
则
所以
（4分）
因为
所以
（5分）
故直线的方程为，抛物线的方程为 （6分）
（II）解法一：据题意，当抛物线过点P的切线与平行时，
的面积最大。（7分）
设点
因为
所以P（-2，-2）。 （9分）此时，点P到直线的距离
（10分） 由
所以
故的面积的最大值为
（12分）
解法二：由（7分）
所以
（8分）
设点
，点P到直线的距离为d。 （9分）
则
当
故的面积的最大值为 （12分）
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
中，
，
，
，
,
与
交于点
． 
；
的大小；
与
所成角的余弦值．
C与平面ABCD所成角的正弦的值；
|x|在x∈[－1,1]的图象上有两点A、B，AB∥
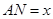（单位：米），若
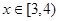（单位：米），则当AM，AN的长度分别是多少时，花坛AMPN的面积最大？并求出最大面积。