题目内容
如果cosα=
,且α为第四象限角,那么tanα的值是
| 1 |
| 2 |
-
| 3 |
-
.| 3 |
分析:由题意可得sinα=-
=-
,再根据 tanα=
求得结果.
| 1-cos2α |
| ||
| 2 |
| sinα |
| cosα |
解答:解:如果cosα=
,且α为第四象限角,那么sinα=-
=-
,tanα=
=-
,
故答案为-
.
| 1 |
| 2 |
| 1-cos2α |
| ||
| 2 |
| sinα |
| cosα |
| 3 |
故答案为-
| 3 |
点评:本题主要考查同角三角函数的基本关系的应用,注意三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
如果cos(π+A)=-
,那么sin(
+A)的值是( )
| 1 |
| 2 |
| π |
| 2 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
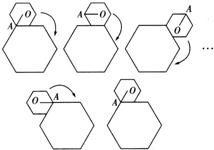 如图,小正六边形沿着大正六边形的边,按顺时针方向滚动.小正六边形的边长是大正六边形边长的一半,如果小正六边形沿着大正六边形的边滚动一周后返回出发时的位置,在这个过程中向量
如图,小正六边形沿着大正六边形的边,按顺时针方向滚动.小正六边形的边长是大正六边形边长的一半,如果小正六边形沿着大正六边形的边滚动一周后返回出发时的位置,在这个过程中向量