题目内容
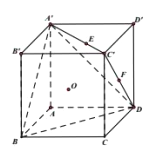
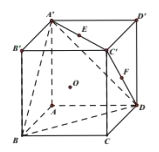
【题目】如图,在正方体![]() 中,
中, ![]() 是
是![]() 的中心,
的中心, ![]() 分别是线段
分别是线段![]() 上的动点,且
上的动点,且![]() ,
, ![]() .
.
(Ⅰ)若直线![]() 平面
平面![]() ,求实数
,求实数![]() 的值;
的值;
(Ⅱ)若![]() ,正方体
,正方体![]() 的棱长为2,求平面
的棱长为2,求平面![]() 和平面
和平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)取![]() 的中点
的中点![]() ,连
,连![]() ,由直线
,由直线![]() 平面
平面![]() 可证得
可证得![]() ,根据平行线分线段成比例定理可得
,根据平行线分线段成比例定理可得![]() ,即
,即![]() ,得到
,得到![]() ;(Ⅱ)建立空间直角坐标系,求出平面
;(Ⅱ)建立空间直角坐标系,求出平面![]() 的法向量
的法向量![]() 、平面
、平面![]() 的法向量
的法向量![]() ,利用向量的夹角求解即可。
,利用向量的夹角求解即可。
试题解析:
(Ⅰ)取![]() 的中点
的中点![]() ,
,
∵![]() 是正
是正![]() 的中心
的中心
∴点![]() 在
在![]() 上,且
上,且![]() ,
,
连![]() ,
,
∵![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(Ⅱ)当![]() 时,点
时,点![]() 分别是
分别是![]() 的中点,以
的中点,以![]() 为原点建立如图所示的空间直角坐标系
为原点建立如图所示的空间直角坐标系![]() ,则
,则![]() 。
。
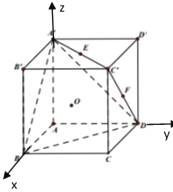
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由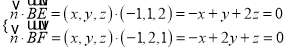 ,
,
得![]() ,令
,令![]() ,得
,得![]() 。
。
同理可得平面![]() 的一个法向量为
的一个法向量为![]()
∴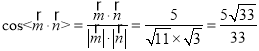 .
.
由图形知,平面![]() 和平面
和平面![]() 所成二面角为锐角,
所成二面角为锐角,
∴平面![]() 和平面
和平面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知函数![]() ,则
,则
(![]() )函数
)函数![]() 定义域为__________.
定义域为__________.
(![]() )函数
)函数![]() 导函数为
导函数为![]() __________.
__________.
(![]() )对函数
)对函数![]() 单调研究如下
单调研究如下
| |||||
|
|
| |||
|
____
(![]() )设函数
)设函数 则
则
函数![]() 的最大值为__________.
的最大值为__________.
(5)函数![]() 极值点共__________个,(6)其中极小值点有__________个.
极值点共__________个,(6)其中极小值点有__________个.
(7)若关于![]() 的方程
的方程![]() 恰有三个不相同的实数解,则
恰有三个不相同的实数解,则![]() 的取值范围为__________.
的取值范围为__________.
【题目】某中学调查了某班全部 45 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加书法社团 | 2 | 30 |
(1)从该班随机选 1 名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的 8 名同学中,有 5 名男同学![]() ,3名女同学
,3名女同学![]() .现从这 5 名男同学和 3 名女同学中各随机选 1 人,求
.现从这 5 名男同学和 3 名女同学中各随机选 1 人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.