题目内容
已知函数f（x）满足f（2x+1）=x2．
（1）求f（x）的解析式；
（2）当1≤x≤2时，g（x）=f（x），求函数y=g（x）的反函数g-1（x）．
解：（1）设t=2x+1，则x=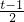
，
代入得：f（t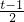）=（）2，
∴
；
（2）∵当1≤x≤2时，g（x）=f（x），
∴y=
（1≤x≤2），
∴x=1+
，（0≤y≤
），
故反函数为
（
．
分析：（1）设t=2x+1，则x=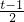，把x代入函数解析式化简后，把t换成x；
（2）由原函数的解析式解出自变量x的解析式，再把x 和y交换位置，注明反函数的定义域（即原函数的值域）．
点评：本题的考点是求函数的解析式的方法，考查函数与反函数的定义，求反函数的方法和步骤，注意反函数的定义域是原函数的值域．
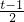，代入得：f（t）=（
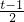）2，∴
；（2）∵当1≤x≤2时，g（x）=f（x），
∴y=
（1≤x≤2），∴x=1+
，（0≤y≤），故反函数为
（．分析：（1）设t=2x+1，则x=
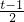，把x代入函数解析式化简后，把t换成x；（2）由原函数的解析式解出自变量x的解析式，再把x 和y交换位置，注明反函数的定义域（即原函数的值域）．
点评：本题的考点是求函数的解析式的方法，考查函数与反函数的定义，求反函数的方法和步骤，注意反函数的定义域是原函数的值域．
练习册系列答案
名校课堂系列答案
相关题目