题目内容
如图所示,AB⊥BC,CD=33,∠ACB=15°,∠BCD=75°,∠BDC=45°,求AB的长.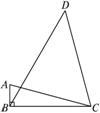
解:在△DBC中,
∠DBC=180°-(∠BDC+∠BCD)=180°-(45°+75°)=60°.
在△BCD中,由正弦定理,得
=
,
∴BC=
=11
.
在Rt△ABC中,AB=BCtan15°=11
(2-
)=22
-33
.
练习册系列答案
相关题目
题目内容
如图所示,AB⊥BC,CD=33,∠ACB=15°,∠BCD=75°,∠BDC=45°,求AB的长.
解:在△DBC中,
∠DBC=180°-(∠BDC+∠BCD)=180°-(45°+75°)=60°.
在△BCD中,由正弦定理,得
=,
∴BC==11.
在Rt△ABC中,AB=BCtan15°=11(2-)=22-33.
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的，其中AB=4，BC=2，CC1=3，BE=1．
在长方体ABCD-A1B1C1D1中，AB=BC=2，过A1，C1，B三点的平面截去长方体的一个角后，得到如图所示的几何体ABCD-A1C1D1，这个几何体的体积为
如图所示，在△ABC中，AD⊥AB，