题目内容
22.已知函数(I)求函数![]() 的解析式;
的解析式;
(II)若对任意的![]() ,恒有f(x)≥x3-mx-11,求
,恒有f(x)≥x3-mx-11,求![]() 的取值范围.
的取值范围.
分析:本小题主要考查函数的性质、导数的应用、不等式的解法等知识,考查数形结合能力以及综合运用数学基本关系解决问题的能力.
(1)解法一:由题设得g(x)=3x2-18xcos![]() +48cosβ,
+48cosβ,
又由1+![]() ∈(1,2],3+sint∈[2,4],
∈(1,2],3+sint∈[2,4],
知g(x)≥0在x∈(1,2]上成立,g(x)≤0在x∈[2,4]上成立,由此易得g(2)=0.
设g(x)=0的另一根为x0.
由y=g(x)的图象为开口向上的抛物线,得x0≥4,而2+x0=6cos![]() ,
,
所以6cos![]() ≥6.
≥6.
又6cos![]() ≤6,得cos
≤6,得cos![]() =1.
=1.
代入g(2)=0,得cosβ=![]() ,即得f(x)=x3-9x2+24x. 6分
,即得f(x)=x3-9x2+24x. 6分
解法二:由题设得g(x)=3x2-18xcos![]() +48cosβ, 2分
+48cosβ, 2分
由g(1+![]() )≥0,g(3+sint)≤0,
)≥0,g(3+sint)≤0,
得g(1+![]() )=g(2)≥0,g(3+sin
)=g(2)≥0,g(3+sin![]() )=g(2)≤0,g(4)=g(3+sin
)=g(2)≤0,g(4)=g(3+sin![]() )≤0,
)≤0,
即有
![]()
由①②得36-36cos![]() ≤0,即1-cos
≤0,即1-cos![]() ≤0.
≤0.
又1-cos![]() ≥0,故cos
≥0,故cos![]() =1.
=1.
代入①得cosβ=![]() ,即得f(x)=x3-9x2+24x.
,即得f(x)=x3-9x2+24x.
(2)解:由题设,知对任意的m∈[-26,6]恒有mx-9x2+24x+11≥0,令h(m)=mx-9x2+24x+11,
则有
解得
即-![]() ≤x≤1.
≤x≤1.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
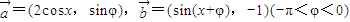 .定义
.定义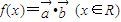 ,且
,且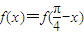 对任意实数x恒成立.
对任意实数x恒成立.