题目内容
已知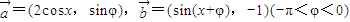 .定义
.定义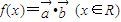 ,且
,且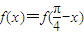 对任意实数x恒成立.
对任意实数x恒成立.(1)求φ的值;
(2)求函数y=f(x)的单调增区间.
【答案】分析:(1)通过向量的数量积,以及角的变换,利用两角和与差的正弦函数化简函数为 一个角的一个三角函数的形式,通过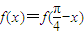 ,推出对称轴,结合φ的范围,求出φ的值.
,推出对称轴,结合φ的范围,求出φ的值.
(2)利用正弦函数的单调增区间直接求出函数y=f(x)的单调增区间.
解答:解:(1)f(x)=2cosxsin(x+ϕ)-sinϕ=2cosxsin(x+ϕ)-sin[(x+ϕ)-x]=sin(x+ϕ)cosx+cosx(x+ϕ)sinx=sin(2x+ϕ).
由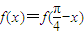 知函数f(x)对称轴是
知函数f(x)对称轴是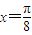 ,即
,即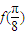 是函数最值
是函数最值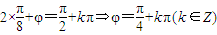 ,又-π<φ<0,所以
,又-π<φ<0,所以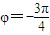 .
.
(2)由(1)知 .
.
由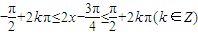 ,解得
,解得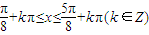 .
.
所以,y=f(x)的单调增区间为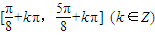 .
.
点评:本题是中档题,通过向量的数量积,考查三角函数的化简解析式的求法,函数的单调增区间的求法,求出φ是本题的关键,常考题型.
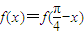 ,推出对称轴,结合φ的范围,求出φ的值.
,推出对称轴,结合φ的范围,求出φ的值.(2)利用正弦函数的单调增区间直接求出函数y=f(x)的单调增区间.
解答:解:(1)f(x)=2cosxsin(x+ϕ)-sinϕ=2cosxsin(x+ϕ)-sin[(x+ϕ)-x]=sin(x+ϕ)cosx+cosx(x+ϕ)sinx=sin(2x+ϕ).
由
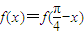 知函数f(x)对称轴是
知函数f(x)对称轴是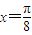 ,即
,即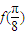 是函数最值
是函数最值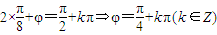 ,又-π<φ<0,所以
,又-π<φ<0,所以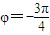 .
.(2)由(1)知
 .
.由
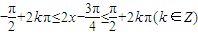 ,解得
,解得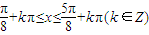 .
.所以,y=f(x)的单调增区间为
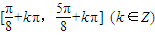 .
.点评:本题是中档题,通过向量的数量积,考查三角函数的化简解析式的求法,函数的单调增区间的求法,求出φ是本题的关键,常考题型.

练习册系列答案
相关题目
 .定义
.定义 ,且
,且 对任意实数x恒成立.
对任意实数x恒成立.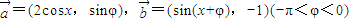 .定义
.定义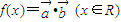 ,且
,且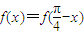 对任意实数x恒成立.
对任意实数x恒成立.