题目内容
（2011•普宁市模拟）已知函数g（x）=2x，且有g（a）g（b）=2，若a＞0且b＞0，则ab的最大值为（ ）
分析：先根据条件得出a+b=1，再应用均值不等式可以把条件转化为关于
的不等式，进而解出ab的取值范围．
| ab |
解答：解：∵函数g（x）=2x，且有g（a）g（b）=2，
∴2a•2b=2⇒a+b=1，
∵a，b∈（0，+∞），
∴a+b ≥2
，即2
≤1，当且仅当a=b时取等号，
解得ab≤
，
故选B．
∴2a•2b=2⇒a+b=1，
∵a，b∈（0，+∞），
∴a+b ≥2
| ab |
| ab |
解得ab≤
| 1 |
| 4 |
故选B．
点评：本题是通过基本不等式，创造所要求的变量，通过解不等式求最大值，属于基础题．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
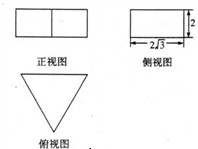（2011•普宁市模拟）若一个正三棱柱的三视图如图所示，则这个正三棱柱的表面积为（ ）
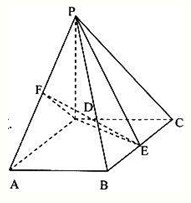（2011•普宁市模拟）如图，四棱锥P-ABCD的底面ABCD为菱形，PD⊥平面ABCD，PD=AD=2，∠BAD=60°，E、F分别为BC、PA的中点．