Question

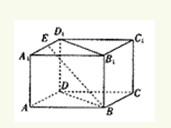（2012•广西模拟）如图，在长方体ABCD-A₁B₁C₁D₁中，AB=BC=2，AA₁=1，E为A₁D₁的中点，则BE与平面BB₁D₁D所成角的正弦值为

3

6

．

Answer 1

分析：过E作EF⊥B₁D₁于F，由DD₁⊥平面A₁B₁C₁D₁，知EF⊥平面BB₁D₁D，连接BF，则∠EBF为BE与平面BB₁D₁D所成角，由在长方体ABCD-A₁B₁C₁D₁中，AB=BC=2，AA₁=1，E为A₁D₁的中点，知EF=

1

4

A1C1=

2

2

，由此能求出BE与平面BB₁D₁D所成角的正弦值．

解答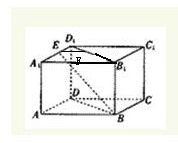：解：过E作EF⊥B₁D₁于F，
∵DD₁⊥平面A₁B₁C₁D₁，
∴DD₁⊥EF，∴EF⊥平面BB₁D₁D，
连接BF，则∠EBF为BE与平面BB₁D₁D所成角，
∵在长方体ABCD-A₁B₁C₁D₁中，AB=BC=2，AA₁=1，E为A₁D₁的中点，
∴EF=

1

4

A1C1=

2

2

，
∵BF=

12+( 3 2 2 )2

=

22

2

，
∴BE=

1 2 + 11 2

=

6

，
∴sin∠EBF=

EF

BE

=

2 2

6

=

3

6

．
故答案为：

3

6

．

点评：本题考查直线与平面所成角的正弦值的求法，解题时要认真审题，仔细解答，注意把空间几何问题合理地转化为平面解析几何问题．