题目内容
在数列{an}中,Sn为其前n项和,a1=1,a2=2,an+2-an=1+(-1)n,则S20= .
【答案】分析:由an+2-an=1+(-1)n,判断出数列的奇数项是常数列,偶数项是等差数列,利用分组的方法将数列{an}分成两个数列,再利用等差数列的前n项和公式求出和.
解答:解:∵an+2-an=1+(-1)n
∴当n为偶数时,an+2-an=2;当n为奇数时,an+2-an=0
∴a1,a3,a5…为各项均为1的常数列;a2,a4,a6…为以2为首项,以2为公差的等差数列
∴S20=((a1+a3+a5…+a19)+(a2+a4+a6+…+a20)=10+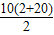 =120
=120
故答案为:120
点评:本题考查数列递推式,考查数列的求和,求得数列的奇数项是常数列,偶数项是等差数列是关键.
解答:解:∵an+2-an=1+(-1)n
∴当n为偶数时,an+2-an=2;当n为奇数时,an+2-an=0
∴a1,a3,a5…为各项均为1的常数列;a2,a4,a6…为以2为首项,以2为公差的等差数列
∴S20=((a1+a3+a5…+a19)+(a2+a4+a6+…+a20)=10+
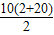 =120
=120故答案为:120
点评:本题考查数列递推式,考查数列的求和,求得数列的奇数项是常数列,偶数项是等差数列是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,S3=12+
,S3=12+ .
. ,
, ,…,
,…, ,…成等比数列,其中n1=1,n2=3,求nk(用k表示);
,…成等比数列,其中n1=1,n2=3,求nk(用k表示);