题目内容
函数 的零点个数为( )
的零点个数为( )
| A.1 | B.2 | C.3 | D.4 |
B
解析试题分析:显然这是一个偶函数,在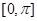 上单调递增,
上单调递增,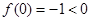 ,
,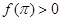 ,所以在
,所以在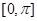 上有一个零点.又
上有一个零点.又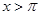 时,
时,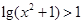 ,而
,而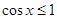 ,所以
,所以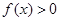 .根据对称性,在
.根据对称性,在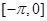 上也有一个零点.所以共有两个零点.
上也有一个零点.所以共有两个零点.
考点:函数的零点.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
已知函数 和
和 都是定义在R上的偶函数,若
都是定义在R上的偶函数,若 时,
时, ,则
,则 为( )
为( )
| A.正数 | B.负数 | C.零 | D.不能确定 |
若函数 满足
满足 且
且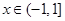 时,
时,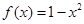 ,函数
,函数 分别在两相邻对称轴
分别在两相邻对称轴 与
与 处取得最值1与-1,则函数
处取得最值1与-1,则函数 在区间
在区间 内零点的个数为( )
内零点的个数为( )
| A.1006 | B.1007 | C.1008 | D.1010 |
下列函数,在其定义域内既是奇函数又是增函数的是 ( )
A.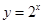  | B.  |
C.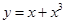  | D.  |
函数f(x)=tan(2x-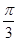 )的单调递增区间是()
)的单调递增区间是()
A.[ , , ](k∈Z) ](k∈Z) |
B.( , , )(k∈Z) )(k∈Z) |
C.[ , , ](k∈Z) ](k∈Z) |
D.( , , )(k∈Z) )(k∈Z) |
已知函数 满足:对定义域内的任意
满足:对定义域内的任意 ,都有
,都有 ,则函数
,则函数 可以是( )
可以是( )
A. | B.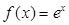 | C. | D. |
 (其中
(其中 ),若
),若 的图象如下图(左)所示,则
的图象如下图(左)所示,则 的图象是 ( )
的图象是 ( )


 x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( ).
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( ).


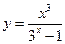 的图象大致是( )
的图象大致是( )