题目内容
己知a∈R,函数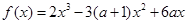
(1)若a=1,求曲线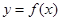 在点(2,f (2))处的切线方程;
在点(2,f (2))处的切线方程;
(2)若|a|>1,求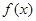 在闭区间[0,|2a|]上的最小值.
在闭区间[0,|2a|]上的最小值.
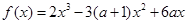
(1)若a=1,求曲线
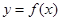 在点(2,f (2))处的切线方程;
在点(2,f (2))处的切线方程;(2)若|a|>1,求
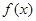 在闭区间[0,|2a|]上的最小值.
在闭区间[0,|2a|]上的最小值.(1) 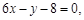 (2) 当
(2) 当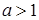 时,函数
时,函数 最小值是
最小值是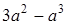 ;当
;当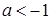 时,函数
时,函数 最小值是
最小值是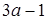 .
.
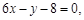 (2) 当
(2) 当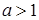 时,函数
时,函数 最小值是
最小值是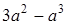 ;当
;当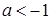 时,函数
时,函数 最小值是
最小值是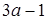 .
.试题分析:(1)由导数的几何意义可知,曲线
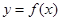 在点(2,f (2))处的导数值为切线的斜率.
在点(2,f (2))处的导数值为切线的斜率. 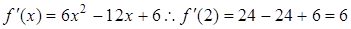 ,当
,当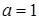 时,
时, 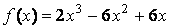
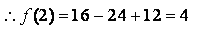 从而
从而 在
在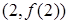 处的切线方程是:
处的切线方程是: 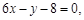 (2)求函数在闭区间上的最值,先要根据导数研究函数单调性,确定其走势,再比较端点及极值点的函数值的大小确定最值. 因为
(2)求函数在闭区间上的最值,先要根据导数研究函数单调性,确定其走势,再比较端点及极值点的函数值的大小确定最值. 因为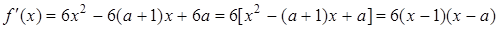 ,所以①当
,所以①当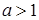 时,
时, 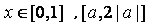 时,
时, 递增,
递增,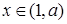 时,
时, 递减,最小值是
递减,最小值是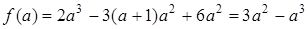 ②当
②当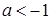 时,
时, 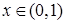 时,
时, 递减,
递减,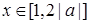 时,
时, 递增,所以最小值是
递增,所以最小值是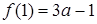 .
.试题解析:(1)当
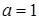 时,
时,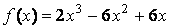
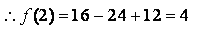 1
1所以
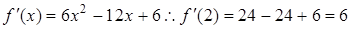 4
4 在
在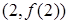 处的切线方程是:
处的切线方程是: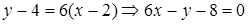 ..6
..6(2)
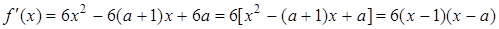 .8
.8 ①当
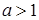 时,
时,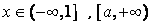 时,
时, 递增,
递增,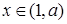 时,
时, 递减
递减所以当
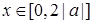 时,且
时,且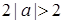 ,
,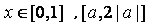 时,
时, 递增,
递增,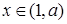 时,
时, 递减 ..10
递减 ..10所以最小值是

②当
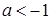 时,且
时,且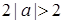 ,在
,在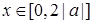 时,
时,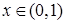 时,
时, 递减,
递减,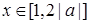 时,
时, 递增,所以最小值是
递增,所以最小值是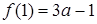
综上所述:当
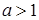 时,函数
时,函数 最小值是
最小值是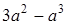 ;
;当
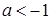 时,函数
时,函数 最小值是
最小值是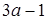 13
13
练习册系列答案
相关题目
 ,
, .
. 在其定义域上为增函数,求
在其定义域上为增函数,求 的取值范围;
的取值范围; 时,函数
时,函数 在区间
在区间 上存在极值,求
上存在极值,求 的最大值.
的最大值. ≈
≈ ).
).
 ,求函数
,求函数 在
在 上的最小值;
上的最小值; 存在单调递增区间,试求实数
存在单调递增区间,试求实数 的取值范围;
的取值范围; 在
在 时有极值10,则
时有极值10,则 的值为( )
的值为( )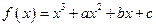 有极值点
有极值点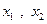 ,且
,且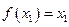 ,则关于x的方程
,则关于x的方程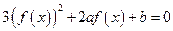 的不同实根个数是( )
的不同实根个数是( )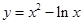 上任意一点,则点P到直线
上任意一点,则点P到直线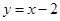 的距离的最小值是
的距离的最小值是 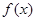 与
与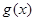 是定义在
是定义在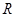 上的两个可导函数,若
上的两个可导函数,若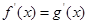 ,则
,则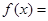
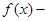
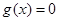
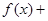
 ,则( )
,则( ) 有最小值
有最小值
