题目内容

若定义域为（-1，1）的奇函数y=f（x）又是减函数，且f（a-3）+f（9-a²）＜0，则实数a的取值范围是________．

$\text{[math]}$
分析：根据f（x）是的奇函数可把不等式f（a-3）+f（9-a²）＜0变形为f（a-3）＜f（a²-9），再根据函数的单调性和定义域解不等式即可．
解答：解；f（a-3）+f（9-a²）＜0可以变形为f（a-3）＜-f（9-a²）
∵y=f（x）是的奇函数，f（a-3）＜f（a²-9）
又∵y=f（x）是定义域为（-1，1）的减函数，
∴ $\text{[math]}$
∴ $\text{[math]}$ ，
∴2 $\text{[math]}$ ＜a＜3
∴实数a的取值范围是 $\text{[math]}$
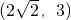
故答案为 $\text{[math]}$
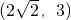
点评：本题主要考查函数奇偶性与单调性的综合应用来解不等式，易错点是忘记考虑函数的定义域．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

已知函数f（x）=

（a为常数且a≠0），定义域为（-1，1）
（1）证明函数f（x）是奇函数；
（2）若a=1，试判断并证明f（x）在（-1，1）上的单调性．

设函数f（x）的定义域为D，若存在非零实数l使得对于任意x∈M（M⊆D），有x+l∈D，且f（x+l）≥f（x），则称f（x）为M上的l高调函数．现给出下列命题：
①函数f（x）=2^-x为R上的1高调函数；
②函数f（x）=sin2x不是R上的π高调函数；
③如果定义域为[-1，+∞）的函数f（x）=x²为[-1，+∞）上m高调函数，那么实数m 的取值范围是[2，+∞）；
④函数f（x）=lg（|x-2|+1）为[1，+∞）上的2高调函数．
其中真命题为

（填序号）．

若定义域为（-1，1）的奇函数y=f（x）又是减函数，且f（a-3）+f（9-a²）＜0，则实数a的取值范围是

若定义域为（-1，1）的奇函数y=f（x）又是减函数，且f（a-3）+f（9-a²）＜0，则实数a的取值范围是______．

若定义域为（-1，1）的奇函数y=f（x）又是减函数，且f（a-3）+f（9-a²）＜0，则实数a的取值范围是．