题目内容
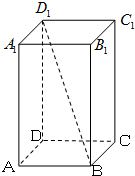
 如图,直四棱柱
如图,直四棱柱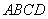 —
—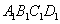 的侧棱
的侧棱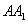 的长是
的长是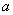 ,底面
,底面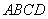 是边长
是边长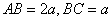 的矩形,
的矩形, 为
为 的中点.
的中点.
⑴ 求证:平面 ⊥平面
⊥平面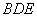 ;
;
⑵ 求二面角E—BD—C的大小;
⑶ 求点C到平面BDE的距离.
【答案】
⑴ 证明:∵直四棱柱 —
—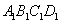 的侧棱
的侧棱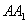 的长是
的长是 ,底面
,底面 是边长
是边长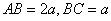 的矩形,
的矩形,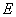 为
为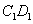 的中点.∴
的中点.∴ ,∴DE⊥CE.
,∴DE⊥CE.
又∵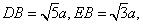 ∴DE⊥EB,∴DE⊥平面CEB,
∴DE⊥EB,∴DE⊥平面CEB,
又∵DE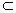 平面
平面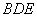 ,∴平面
,∴平面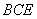 ⊥平面
⊥平面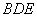 。-----------4分
。-----------4分
⑵ 取DC的中点F(如图),则EF⊥平面BCD.作FH⊥BD,垂足为H,连接EH,易知FH为EH在平面BCD内的射影,由三垂线定理知EH⊥BD,故∠EHF就是二面角E—BD—C的一个平面角.
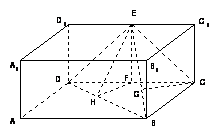 由题意得EF=
由题意得EF= ,HF=
,HF=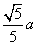 ,
,
在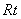 △EFH中,
△EFH中,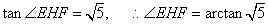 .
.
故二面角E—BD—C的大小为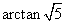 .----------8分
.----------8分
⑶ 作CG⊥EB,垂足为G.由⑴知平面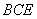 ⊥平面
⊥平面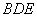 ,则CG⊥平面BDE,线段CG之长即为点C到平面BDE的距离.
,则CG⊥平面BDE,线段CG之长即为点C到平面BDE的距离.
∵BC⊥平面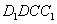 ,∴BC⊥CE.在
,∴BC⊥CE.在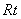 △ECB中,
△ECB中,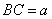 ,
,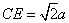 ,
, .
.
∴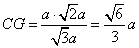 ,故点C到平面BDE的距离为
,故点C到平面BDE的距离为 .-----------12分
.-----------12分

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,直四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧棱长
如图,直四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧棱长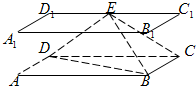 如图,直四棱柱ABCD-A1B1C1D1的侧棱AA1的长为a,底面ABCD是边长AB=2a,BC=a的矩形,E为C1D1的中点.
如图,直四棱柱ABCD-A1B1C1D1的侧棱AA1的长为a,底面ABCD是边长AB=2a,BC=a的矩形,E为C1D1的中点. 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.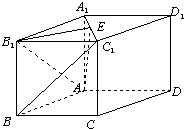 如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为a的菱形,且∠ABC=60°,侧棱长为
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为a的菱形,且∠ABC=60°,侧棱长为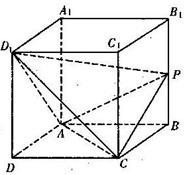 如图,直四棱柱ABCD-A1B2C3D4中,侧棱AA1=2,底面ABCD是菱形,AB=2,∠ABC=60°,P为侧棱BB1上的动点.
如图,直四棱柱ABCD-A1B2C3D4中,侧棱AA1=2,底面ABCD是菱形,AB=2,∠ABC=60°,P为侧棱BB1上的动点.