题目内容
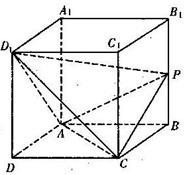 如图,直四棱柱ABCD-A1B2C3D4中,侧棱AA1=2,底面ABCD是菱形,AB=2,∠ABC=60°,P为侧棱BB1上的动点.
如图,直四棱柱ABCD-A1B2C3D4中,侧棱AA1=2,底面ABCD是菱形,AB=2,∠ABC=60°,P为侧棱BB1上的动点.(1)求证:D1P⊥AC;
(2)当二面角D1-AC-P的大小为120°,求BP的长;
(3)在(2)的条件下,求三棱锥P-ACD1的体积.
分析:(1)应通过证明AC⊥平面BB1D1D得出D1P⊥AC;
(2)易知∠D1OP是二面角D1-AC-P的平面角,设BP=x(0≤x≤2),在△D1OP中,由余弦定理建立关于x的方程求解计算即可.
(3)在(1)的基础上,考虑将三棱锥P-ACD1分割成A-OPD1与C-OPD1,转化求解.
另可以设上、下底面菱形对角线交点分别为O1,O,以O为原点,建立空间直角坐标系,利用空间向量的方法解决(1),(2).
(2)易知∠D1OP是二面角D1-AC-P的平面角,设BP=x(0≤x≤2),在△D1OP中,由余弦定理建立关于x的方程求解计算即可.
(3)在(1)的基础上,考虑将三棱锥P-ACD1分割成A-OPD1与C-OPD1,转化求解.
另可以设上、下底面菱形对角线交点分别为O1,O,以O为原点,建立空间直角坐标系,利用空间向量的方法解决(1),(2).
解答:解法一:(1)连接BD,则AC⊥BD,
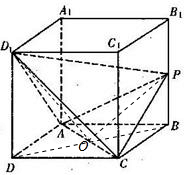
∵D1D⊥底面ABCD,∴AC⊥D1D …(2分)
∴AC⊥平面BB1D1D,
∵D1P?平面BB1D1D,∴D1P⊥AC.…(4分)
(2)设AC∩BD=O,
连接D1O,OP,
∵D1A=D1C,∴D1O⊥AC,同理PO⊥AC,
∴∠D1OP是二面角D1-AC-P的平面角.…(6分)
∴∠D1OP=120°.
设BP=x(0≤x≤2),
∵AB=2,∠ABC=60°,则BO=DO=
,
∴PO=
,D1O=
=
.
在RT△D1B1P1中,D1P=
.
在△D1OP中,由余弦定理D1P2=D1O2+PO2-2D1O•PO•cos120°得
12+(2-x)2=7+3+x2+2
•
,
即6-4x=
整理得3x2-16x+5=,解得x=
,或x=5(舍).∴BP=
,.…(9分)
(3)∵BP=
,,∴PO=
=
,
∴S△POD1=
•PO•OD1•sin120°=
•
•
=
.
∵AC⊥平面OPD1,
∴VP-ACD1的=VP-OCD1 +VP-OAD1=V A-OPD1+V C-OPD1
=
S△POD1•AC=
•=
•2=
.
解法二:设上、下底面菱形对角线交点分别为O1,O,
则AC⊥BD,OO1⊥平面ABCD.
如图,以OD、OC、OO1所在直线为xyz轴,建立空间直角坐标系.…(1分)
(1)A(1,-1,0),C(0,1,0),D1(
,0,2),B(-
,0,0)
设P(-
,0,x)(0≤x≤2)则
=(0,2,0),
=(-2
,0,x-2),则
•
=0
∴
⊥
=0即AC⊥D1P.…(5分)
(2)
=(
,0,2),
=(-
,0,x),
•
=0,
•
=0.
⊥
,
⊥
∴<
,
>就是二面角D1-AC-P的平面角,…(7分)
cos∠D1OP=
=
=-
.
解得x=
,或x=5(舍).
∴BP=
,…(9分)
(3)同解法一.

∵D1D⊥底面ABCD,∴AC⊥D1D …(2分)
∴AC⊥平面BB1D1D,
∵D1P?平面BB1D1D,∴D1P⊥AC.…(4分)
(2)设AC∩BD=O,
连接D1O,OP,
∵D1A=D1C,∴D1O⊥AC,同理PO⊥AC,
∴∠D1OP是二面角D1-AC-P的平面角.…(6分)
∴∠D1OP=120°.
设BP=x(0≤x≤2),
∵AB=2,∠ABC=60°,则BO=DO=
| 3 |
∴PO=
| 3+x2 |
| 4+3 |
| 7 |
在RT△D1B1P1中,D1P=
| 12+(2-x)2 |
在△D1OP中,由余弦定理D1P2=D1O2+PO2-2D1O•PO•cos120°得
12+(2-x)2=7+3+x2+2
| 7 |
| 3+x2 |
| 1 |
| 2 |
即6-4x=
| 7(3+x2) |
整理得3x2-16x+5=,解得x=
| 1 |
| 3 |
| 1 |
| 3 |
(3)∵BP=
| 1 |
| 3 |
3+
|
2
| ||
| 3 |
∴S△POD1=
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
| 7 |
| ||
| 2 |
7
| ||
| 6 |
∵AC⊥平面OPD1,
∴VP-ACD1的=VP-OCD1 +VP-OAD1=V A-OPD1+V C-OPD1
=
| 1 |
| 3 |
| 1 |
| 3 |
7
| ||
| 6 |
7
| ||
| 9 |
解法二:设上、下底面菱形对角线交点分别为O1,O,
则AC⊥BD,OO1⊥平面ABCD.
如图,以OD、OC、OO1所在直线为xyz轴,建立空间直角坐标系.…(1分)

(1)A(1,-1,0),C(0,1,0),D1(
| 3 |
| 3 |
设P(-
| 3 |
| AC |
| D1P |
| 3 |
| AC |
| D1P |
∴
| AC |
| D1P |
(2)
| OD1 |
| 3 |
| OP |
| 3 |
| OD1 |
| AC |
| OP |
| AC |
| OD1 |
| AC |
| OP |
| AC |
∴<
| OD1 |
| OP |
cos∠D1OP=
| ||||
|
|
| 2x-3 | ||||
|
| 1 |
| 2 |
解得x=
| 1 |
| 3 |
∴BP=
| 1 |
| 3 |
(3)同解法一.
点评:本题考查异面直线夹角,二面角大小求解,考查考查空间想象、推理论证能力.利用空间向量的方法,能降低思维难度,思路相对固定,是人们研究解决几何体问题又一有力工具

练习册系列答案
相关题目
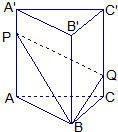 如图:直三棱柱ABC-A′B′C′的体积为V,点P、Q分别在侧棱AA′和CC′上,AP=C′Q,则四棱锥B-APQC的体积为
如图:直三棱柱ABC-A′B′C′的体积为V,点P、Q分别在侧棱AA′和CC′上,AP=C′Q,则四棱锥B-APQC的体积为 如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2.
如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2. 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8. (2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.
(2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点. 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.