题目内容
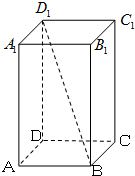如图，直四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形，侧棱长AA1=| 2 |
| π |
| 3 |
| π |
| 3 |
分析：根据异面直线所成角的定义，证明已知角为异面直线所成的角，再解三角形求角即可．
解答：
解：连接BC1，∵A1B1∥C1D1，
∴∠BD1C1为异面直线A1B1与BD1所成的角，
∵直四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形，
∴C1D1⊥平面BCC1B1，
∴C1D1⊥BC1，
在Rt△BC1D1中，BC1=
，tan∠BD1C1=
=
，
∠BD1C1=
．
故答案是
解：连接BC1，∵A1B1∥C1D1，∴∠BD1C1为异面直线A1B1与BD1所成的角，
∵直四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形，
∴C1D1⊥平面BCC1B1，
∴C1D1⊥BC1，
在Rt△BC1D1中，BC1=
| 3 |
| BC1 |
| C1D1 |
| 3 |
∠BD1C1=
| π |
| 3 |
故答案是
| π |
| 3 |
点评：本题考查异面直线所成的角．异面直线所成的角的求法是：1、作角（作平行线）；2、证角（符合定义）；3、求角（解三角形）．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
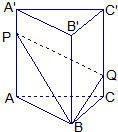如图：直三棱柱ABC-A′B′C′的体积为V，点P、Q分别在侧棱AA′和CC′上，AP=C′Q，则四棱锥B-APQC的体积为
如图，直三棱柱ABC-A1B1C1中，AB⊥BC，D为AC的中点，AA1=AB=2．
如图，直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形，∠ABC=45°，其侧面展开图是边长为8的正方形．E、F分别是侧棱AA1、CC1上的动点，AE+CF=8．
（2012•房山区二模）如图，直四棱柱ABCD-A1B1C1D1中，底面ABCD是菱形，且∠ABC=60°，E为棱CD的中点．
如图，在四棱柱ABC-A1B1C1D1中，AA1⊥底面ABCD，底面ABCD是菱形，∠DAB=60°，AA1=4，AB=2，点E在棱CC1上，点E是棱C1C上一点．