题目内容
如图4,已知四棱锥 ,底面
,底面 是正方形,
是正方形, 面
面 ,点
,点 是
是 的中点,点
的中点,点 是
是 的中点,连接
的中点,连接 ,
,
 .
.
(1) 求证: 面
面 ;
;
(2)若 ,
, ,求二面角
,求二面角 的余弦值.
的余弦值.
 |
 (1)证法1:取
(1)证法1:取 的中点
的中点 ,连接
,连接 ,
,
∵点 是
是 的中点,
的中点,
∴ .
.
∵点 是
是 的中点,底面
的中点,底面 是正方形,
是正方形,
∴ .
.
∴ .
.
∴四边形 是平行四边形.
是平行四边形.
∴ . …
. …
 ∵
∵ 平面
平面 ,
, 平面
平面 ,
,
∴ 面
面 . …………… 4分
. …………… 4分
证法2:连接 并延长交
并延长交 的延长线于点
的延长线于点 ,连接
,连接 ,
,
∵点 是
是 的中点,
的中点,
∴ ,
,
∴点 是
是 的中点.
的中点.
∵点 是
是 的中点,
的中点,
∴ .
.
∵ 面
面 ,
, 平面
平面 ,
,
∴ 面
面 .
.
证法3: 取 的中点
的中点 ,连接
,连接 ,
,
∵点 是
是 的中点,点
的中点,点 是
是 的中点,
的中点,
∴ ,
, .
.
∵ 面
面 ,
, 平面
平面 ,
,
∴ 面
面 .
.
∵ 面
面 ,
, 平面
平面 ,
,
∴ 面
面 .
.
 ∵
∵ ,
, 平面
平面 ,
, 平面
平面 ,
,
∴平面 面
面 .
.
∵ 平面
平面 ,
,
∴ 面
面 .
.
…(2)解法1:∵ ,
, 面
面 ,
,
∴ 面
面 .
.
∵ 面
面 ,
,
∴ . …
. …
过 作
作 ,垂足为
,垂足为 ,连接
,连接 ,
,
∵ ,
, 面
面 ,
, 面
面 ,
,
∴ 面
面 .
.
∵ 面
面 ,
,
∴ .
.
∴ 是二面角
是二面角 的平面角.
的平面角.
在Rt△ 中,
中, ,
, ,得
,得 ,
,
在Rt△ 中,
中, ,得
,得 ,
,
 .
.
在Rt△ 中,
中, ,
,
 .
.
∴二面角 的余弦值为
的余弦值为 .
.
解法2:∵ ,
, 面
面 ,
,
∴ 面
面 .
.
在Rt△ 中,
中, ,
, ,得
,得 ,
,
…………… 5分
以点 为原点,
为原点, 所在直线为
所在直线为 轴,
轴, 所在直线为
所在直线为 轴,
轴, 所在直线为
所在直线为 轴,
轴,
建立空间直角坐标系 ,
,
则 .
.
∴ ,,
,, .
.
设平面 的法向量为
的法向量为
 ,
,
由
 ,
,
 ,
,
 得
得
令 ,得
,得 ,
, .
.
∴
 是平面
是平面 的一个法向量.
的一个法向量.
又 是平面
是平面 的一个法向量,
的一个法向量,



 .
.
∴二面角 的余弦值为
的余弦值为 . …
. …

 名校课堂系列答案
名校课堂系列答案对于函数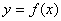 ,部分
,部分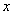 与
与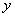 的对应关系如下表:
的对应关系如下表:
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|
| 7 | 4 | 5 | 8 | 1 | 3 | 5 | 2 | 6 |
数列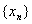 满足
满足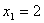 ,且对任意
,且对任意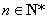 ,点
,点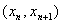 都在函数
都在函数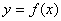 的图象上,则
的图象上,则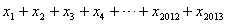 的值为
的值为
(A)9394 (B)9380 (C)9396 (D)9400
 C.19 D .21
C.19 D .21 的三视图如图1所示,则四棱锥
的三视图如图1所示,则四棱锥 B.
B. C.
C. D.
D.

 的值是 .
的值是 .
 ,则实数
,则实数 的值为
的值为 B.
B. C.
C. D.
D.
 为虚数单位,计算
为虚数单位,计算 .
.  上的函数
上的函数 的对称轴为
的对称轴为 ,且当
,且当 时,
时, .若函数
.若函数 (
( )上有零点,则
)上有零点,则 的值为
的值为 或
或 (B)
(B) (C)
(C) 或
或