题目内容
(本小题满分12分)如图,椭圆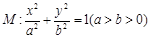 的离心率为
的离心率为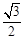 ,直线
,直线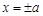 和
和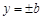 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.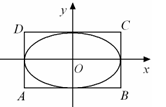
(Ⅰ)求椭圆M的标准方程;
(Ⅱ) 设直线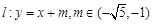 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点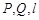 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点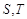 .求
.求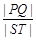 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.
(I) 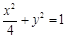 .(II)
.(II) 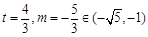 时,
时,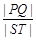 取得最大值
取得最大值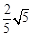 .
.
解析试题分析:(1)根据已知中的离心率和矩形的面积得到a,b,c的方程,进而求解椭圆方程。
(2)将已知中的直线方程与椭圆方程联立方程组,结合韦达定理得到根与系数的关系,那么得到弦长公式,同时以及得到点S,T的坐标,进而得到比值。
(I)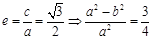 ……①
……①
矩形ABCD面积为8,即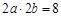 ……②
……②
由①②解得: , ∴椭圆M的标准方程是
, ∴椭圆M的标准方程是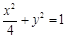 .
.
(II)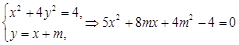 ,
,
设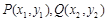 ,则
,则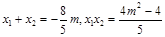 ,
,
当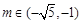

 .
.
当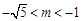 时,有
时,有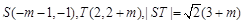 ,
,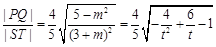 ,
,
其中 ,由此知当
,由此知当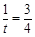 ,即
,即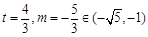 时,
时,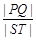 取得最大值
取得最大值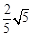 .
.
考点:本试题主要考查了椭圆方程的求解以及直线与椭圆位置关系的综合运用。
点评:解决该试题的关键是运用代数的方法来解决解析几何问题时,解析几何的本质。能结合椭圆的性质得到其方程,并联立方程组,结合韦达定理和判别式的到比值。

练习册系列答案
相关题目
 的右焦点F为
的右焦点F为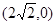 ,G上的点到点F的最大距离为
,G上的点到点F的最大距离为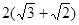 ,斜率为1的直线
,斜率为1的直线 与椭圆G交与
与椭圆G交与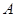 、
、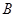 两点,以AB为底边作等腰三角形,顶点为P(-3,2)
两点,以AB为底边作等腰三角形,顶点为P(-3,2)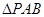 的面积。
的面积。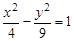 有相同的渐近线,且一条准线为
有相同的渐近线,且一条准线为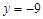 ,求双曲线C的方程;
,求双曲线C的方程; (Ⅱ)已知圆截
(Ⅱ)已知圆截 轴所得弦长为6,圆心在直线
轴所得弦长为6,圆心在直线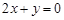 上,并与
上,并与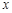 轴相切,求该圆的方程.
轴相切,求该圆的方程.  ,焦点到渐近线的距离为
,焦点到渐近线的距离为 ,求此双曲线的方程.
,求此双曲线的方程.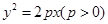 过点A
过点A 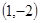
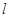 过定点
过定点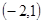 ,斜率为
,斜率为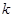 ,当
,当 =1(a>b>o)的离心率e=
=1(a>b>o)的离心率e= ,且经过点(
,且经过点( ,1),O为坐标原点。
,1),O为坐标原点。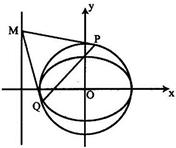
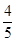 PD.
PD.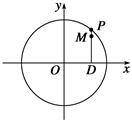
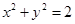 交
交 轴于A,B两点,曲线C是以
轴于A,B两点,曲线C是以 为长轴,离心率为
为长轴,离心率为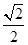 的椭圆,其左焦点为F.若P是圆O上一点连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.
的椭圆,其左焦点为F.若P是圆O上一点连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.
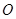 相切;
相切;