题目内容
已知椭圆G: 的右焦点F为
的右焦点F为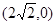 ,G上的点到点F的最大距离为
,G上的点到点F的最大距离为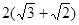 ,斜率为1的直线
,斜率为1的直线 与椭圆G交与
与椭圆G交与 、
、 两点,以AB为底边作等腰三角形,顶点为P(-3,2)
两点,以AB为底边作等腰三角形,顶点为P(-3,2)
(1)求椭圆G的方程;
(2)求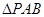 的面积。
的面积。
(1) ; (2)
; (2) 。
。
解析试题分析:(1)因为椭圆G: 的右焦点F为
的右焦点F为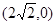 ,所以c=
,所以c= ,
,
因为G上的点到点F的最大距离为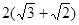 ,所以a+c=
,所以a+c=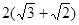 ,又因为
,又因为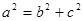 ,所以a=
,所以a=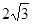 ,b=2,c=
,b=2,c= ,所以椭圆G的方程为
,所以椭圆G的方程为 。
。
(2)易知直线 的斜率存在,所以设直线
的斜率存在,所以设直线 为:
为: ,联立椭圆方程
,联立椭圆方程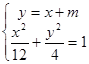 得:
得: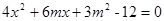 ,设
,设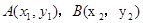 ,则
,则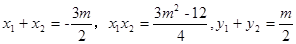 ,
,
过点P(-3,2)且与 垂直的直线为:
垂直的直线为: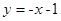 ,A、B的中点M在此直线上,所以
,A、B的中点M在此直线上,所以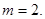
所以A、B的中点坐标为M(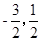 ),所以|PM|=
),所以|PM|=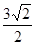 ,
,
又|AB|=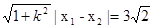 ,所以S=
,所以S=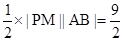 。
。
考点:本题考查椭圆的标准方程:直线与椭圆的综合应用。
点评:椭圆上的一点到焦点的最大距离 =" a+c" ,最小距离 =" a-c" ,到焦点距离最大点和最小点是椭圆长轴的端点。

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 ,长轴长为
,长轴长为 ,离心率
,离心率 ,过右焦点
,过右焦点 的直线
的直线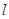 交
交 ,
, 两点:
两点: 的面积;
的面积; 是椭圆
是椭圆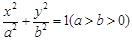 上一点,
上一点, ,
, 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足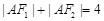
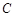 、
、 是椭圆上任两点,且直线
是椭圆上任两点,且直线 、
、 的斜率分别为
的斜率分别为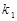 、
、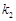 ,若存在常数
,若存在常数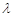 使
使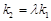 ,求直线
,求直线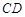 的斜率.
的斜率. 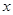 轴上,左右焦点分别为
轴上,左右焦点分别为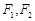 ,且
,且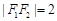 ,
,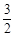 )在椭圆C上.
)在椭圆C上.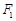 的直线
的直线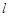 与椭圆
与椭圆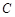 相交于
相交于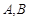 两点,且
两点,且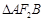 的面积为
的面积为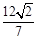 ,求直线
,求直线 轴的负半轴上,过点
轴的负半轴上,过点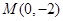 作直线
作直线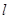 与抛物线交于A,B两点,且满足
与抛物线交于A,B两点,且满足 ,
,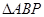 面积的的最大值.
面积的的最大值.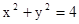 上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线
上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线 、抛物线
、抛物线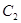 的焦点是直线y=x-1与x轴的交点.
的焦点是直线y=x-1与x轴的交点.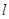 满足条件:① 过
满足条件:① 过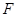 ;②与
;②与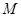 ,
,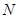 ,且满足
,且满足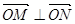 ?若存在,求出直线
?若存在,求出直线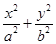 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+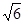 =0相切。
=0相切。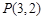 ,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程.
,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程. 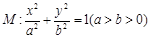 的离心率为
的离心率为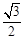 ,直线
,直线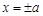 和
和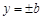 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.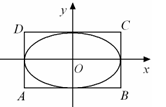
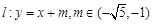 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点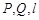 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点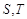 .求
.求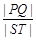 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.