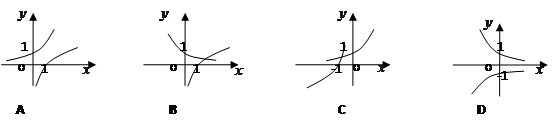题目内容
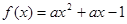 在
在 上恒满足
上恒满足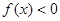 ,则
,则 的取值范围是
的取值范围是
A.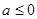 | B.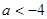 | C.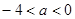 | D.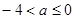 |
D
解析试题分析:当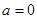 时,
时,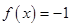 满足在
满足在 上恒有
上恒有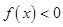 ,当
,当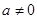 时需满足
时需满足
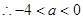 综上得
综上得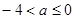
考点:函数性质及最值
点评:本题中需对 分情况讨论,其中
分情况讨论,其中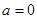 容易被忽略
容易被忽略

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
若定义在R上的偶函数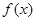 满足
满足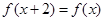 ,且当
,且当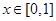 时,
时,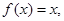 则方程
则方程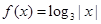 的解个数是 ( )
的解个数是 ( )
| A.0个 | B.2个 | C.4个 | D.6个 |
设函数 为定义在R上的奇函数,当
为定义在R上的奇函数,当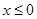 时,
时, (
( 为常数),则
为常数),则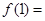 ( )
( )
| A.3 | B.1 | C.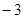 | D. |
下列各组函数中表示同一函数的是( )
A.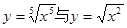 | B.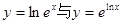 |
C. | D.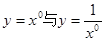 |
函数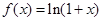 的定义域是( )
的定义域是( )
A.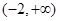 | B.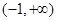 | C.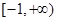 | D.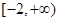 |
已知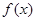 在
在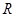 上是减函数,则满足
上是减函数,则满足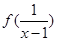 >
> 的实数
的实数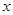 的取值范围是( ).
的取值范围是( ).
| A.(-∞,1) | B.(2,+∞) |
| C.(-∞,1)∪(2,+∞) | D.(1,2) |
若函数 在区间
在区间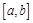 上为减函数,则
上为减函数,则 在
在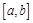 上( ).
上( ).
| A.至少有一个零点 | B.只有一个零点 |
| C.没有零点 | D.至多有一个零点 |
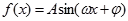 (
(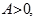
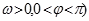 的部分图像如图所示.若△EFG为等腰直角三角形,且
的部分图像如图所示.若△EFG为等腰直角三角形,且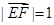 ,则
,则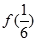 的值为 ( )
的值为 ( )

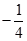
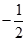
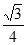
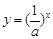 与
与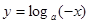 (其中
(其中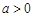 且
且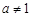 )的图象只可能是( )
)的图象只可能是( )