题目内容
若P是双曲线C1:| x2 |
| a2 |
| y2 |
| b2 |
分析:a2+b2=c2,知圆C2必过双曲线C1的两个焦点,∠F1PF2=
,2∠PF1F2=∠PF2F1=
,则|PF2|=c,|PF1| =
c,由此能求出双曲线的离心率.
| π |
| 2 |
| π |
| 3 |
| 3 |
解答:解:∵a2+b2=c2,
∴圆C2必过双曲线C1的两个焦点,∠F1PF2=
,
2∠PF1F2=∠PF2F1=
,则|PF2|=c,|PF1| =
c,
故双曲线的离心率为
=
+1.
故答案为:
+1.
∴圆C2必过双曲线C1的两个焦点,∠F1PF2=
| π |
| 2 |
2∠PF1F2=∠PF2F1=
| π |
| 3 |
| 3 |
故双曲线的离心率为
| 2c | ||
|
| 3 |
故答案为:
| 3 |
点评:本题考查双曲线的性质和应用,解题时要认真审题,注意挖掘题设中的隐含条件.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
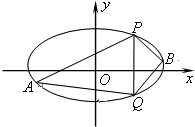 已知中心在坐标原点,坐标轴为对称轴的椭圆C和等轴双曲线C1,点
已知中心在坐标原点,坐标轴为对称轴的椭圆C和等轴双曲线C1,点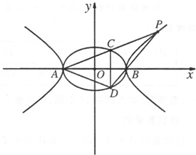 (2012•湛江二模)已知椭圆C1:
(2012•湛江二模)已知椭圆C1: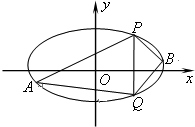 已知中心在坐标原点,坐标轴为对称轴的椭圆C和等轴双曲线C1,点
已知中心在坐标原点,坐标轴为对称轴的椭圆C和等轴双曲线C1,点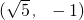 在曲线C1上,椭圆C的焦点是双曲线C1的顶点,且椭圆C与y轴正半轴的交点M到直线
在曲线C1上,椭圆C的焦点是双曲线C1的顶点,且椭圆C与y轴正半轴的交点M到直线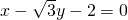 的距离为4.
的距离为4. ,求四边形APBQ面积的最大值.
,求四边形APBQ面积的最大值.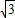 )的双曲线C1上的一动点,点Q是P关于双曲线C1实轴A1A2的对称点,设直线PA1与QA2的交点为M(x,y),
)的双曲线C1上的一动点,点Q是P关于双曲线C1实轴A1A2的对称点,设直线PA1与QA2的交点为M(x,y),