题目内容
已知正项数列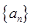 中,其前
中,其前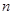 项和为
项和为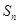 ,且
,且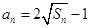 .
.
(1)求数列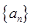 的通项公式;
的通项公式;
(2)设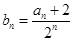 ,
,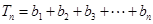 ,求证:
,求证: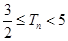 ;
;
(3)设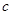 为实数,对任意满足成等差数列的三个不等正整数
为实数,对任意满足成等差数列的三个不等正整数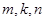 ,不等式
,不等式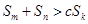 都成立,求实数
都成立,求实数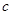 的取值范围.
的取值范围.
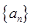 中,其前
中,其前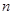 项和为
项和为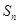 ,且
,且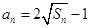 .
.(1)求数列
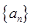 的通项公式;
的通项公式;(2)设
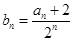 ,
,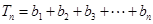 ,求证:
,求证: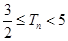 ;
;(3)设
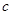 为实数,对任意满足成等差数列的三个不等正整数
为实数,对任意满足成等差数列的三个不等正整数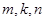 ,不等式
,不等式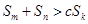 都成立,求实数
都成立,求实数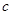 的取值范围.
的取值范围.(1) ;(2)证明过程详见解析;(3)
;(2)证明过程详见解析;(3) .
.
 ;(2)证明过程详见解析;(3)
;(2)证明过程详见解析;(3) .
.试题分析:本题主要考查等差数列的通项公式、前n项和公式、错位相减法、恒成立问题、基本不等式等基础知识,考查学生的分析问题解决问题的能力、计算能力、转化能力.第一问,法一,利用
 转化已知表达式中的
转化已知表达式中的 ,证明数列
,证明数列 为等差数列,通过
为等差数列,通过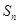 ,再求
,再求 ;法二,利用
;法二,利用 转化
转化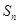 ,证明数列
,证明数列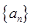 为等差数列,直接得到
为等差数列,直接得到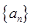 的通项公式;第二问,结合第一问的结论,利用错位相减法证明不等式的右侧,而
的通项公式;第二问,结合第一问的结论,利用错位相减法证明不等式的右侧,而 ,利用放缩法,得
,利用放缩法,得 ,从而证明了不等式的左边,即得证;第三问,利用等差中项的概念得到m,n,k的关系,先将不等式
,从而证明了不等式的左边,即得证;第三问,利用等差中项的概念得到m,n,k的关系,先将不等式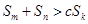 都成立转化为
都成立转化为 ,则关键是求出
,则关键是求出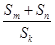 的最小值,利用基本不等式求函数最值.
的最小值,利用基本不等式求函数最值.(1)法一:由
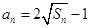 得
得当
 时,
时, ,且
,且 ,故
,故 1分
1分当
 时,
时, ,故
,故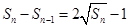 ,得
,得 ,
,∵正项数列
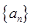 ,
,∴

∴
 是首项为
是首项为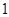 ,公差为
,公差为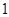 的等差数列. 4分
的等差数列. 4分∴
 ,
,
∴
 . 5分
. 5分法二:
当
 时,
时, ,且
,且 ,故
,故 1分
1分由
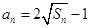 得
得 ,
,当
 时,
时,
∴

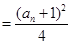
 ,整理得
,整理得
∵正项数列
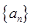 ,
, ,
,∴
 , 4分
, 4分∴
 是以
是以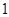 为首项,
为首项, 为公差的等差数列,
为公差的等差数列,∴
 . 5分
. 5分(2)
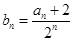

∴
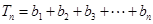

∴

∴两式相减得


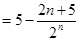 8分
8分∵
 ,∴
,∴
∵
 ∴
∴
∴
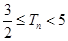 10分
10分(3)∵不等正整数
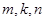 是等差数列,
是等差数列,∴
 ,
,∴
 , 11分
, 11分又
 ,
,∴

故实数
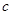 的取值范围为
的取值范围为 . 14分
. 14分
练习册系列答案
相关题目
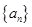 和
和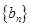 满足:
满足: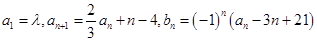 ,其中
,其中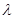 为实数,
为实数,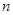 为正整数.
为正整数.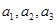 不成等比数列;
不成等比数列;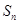 为数列
为数列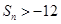 ?若存在,求
?若存在,求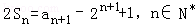 ,且a1,a2+5,a3成等差数列.
,且a1,a2+5,a3成等差数列.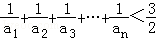 .
.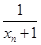 -1,则x2014=( )
-1,则x2014=( )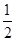
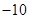 的等差数列,从第
的等差数列,从第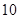 项起开始为正数,则公差
项起开始为正数,则公差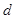 的取值范围是( ).
的取值范围是( ). 



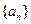 的公差大于零的等差数列,已知
的公差大于零的等差数列,已知 ,
, .
. 是以函数
是以函数 的最小正周期为首项,以
的最小正周期为首项,以 为公比的等比数列,求数列
为公比的等比数列,求数列 的前
的前 项和
项和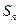 .
. }是等差数列,数列{
}是等差数列,数列{ }的前
}的前 项和
项和 满足
满足 ,
, ,
, 。
。 为数列{
为数列{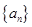 前15项的和
前15项的和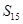 =30,则
=30,则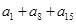 =___________.
=___________.