题目内容
设函数f(x)=sin2x+acosx+| 5 |
| 8 |
| 3 |
| 2 |
| π |
| 2 |
分析:利用平方关系化简函数f(x)=sin2x+acosx+
a-
为:-(cosx-
)2+
(2a2+5a-4);然后比较
与cosx的大小,即对a讨论:0≤a≤2,a>2,a<0,分别利用函数的最大值为1,求出符合题意的a的值即可.
| 5 |
| 8 |
| 3 |
| 2 |
| a |
| 2 |
| 1 |
| 8 |
| a |
| 2 |
解答:解:.f(x)=1-cos2x+acosx+
a-
=-(cosx-
)2+
(2a2+5a-4),
x∈[0,
],∴cosx∈[0,1]
(1)若0≤
≤1,即0≤a≤2,
当cosx=
时,f(x)最大.此时
(2a2+5a-4)=1
解得a=
(2))若
>1,即a>2,当x=0时,即cosx=1时,f(x)最大.
此时-(1-
)2
(2a2+5a-4)=1
a=
(不符和条件)
(3)若
<0,即a<0,a=-4(舍)或a=
,
当x=
时,f(x)最大.此时-(0-
)2+
(2a2+5a-4)=1
a=
(不符和条件)
综上可得:a=
| 5 |
| 8 |
| 3 |
| 2 |
| a |
| 2 |
| 1 |
| 8 |
x∈[0,
| π |
| 2 |
(1)若0≤
| a |
| 2 |
当cosx=
| a |
| 2 |
| 1 |
| 8 |
解得a=
| 3 |
| 2 |
(2))若
| a |
| 2 |
此时-(1-
| a |
| 2 |
| 1 |
| 8 |
a=
| 20 |
| 13 |
(3)若
| a |
| 2 |
| 3 |
| 2 |
当x=
| π |
| 2 |
| a |
| 2 |
| 1 |
| 8 |
a=
| 12 |
| 5 |
综上可得:a=
| 3 |
| 2 |
点评:本题考查三角函数的最值,考查分类讨论思想,0≤a≤2,a>2,a<0是怎么得到的(比较
与cosx的大小),是解题的关键.本题是中档题.
| a |
| 2 |

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 )-cos2(x+
)-cos2(x+ )(x∈R),则函数f(x)是( )
)(x∈R),则函数f(x)是( ) 的奇函数
的奇函数 的偶函数
的偶函数 sinωx•cosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
sinωx•cosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈( ,1).
,1). ,求函数f(x)的值域.
,求函数f(x)的值域.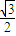 -
- sin2ωx-sinωxcosωx(ω>0),且y=f(x)的图象的一个对称中心到最近的对称轴的距离为
sin2ωx-sinωxcosωx(ω>0),且y=f(x)的图象的一个对称中心到最近的对称轴的距离为 ,
, ]上的最大值和最小值.
]上的最大值和最小值.