题目内容
8.设x,y满足约束条件$\left\{\begin{array}{l}x+y-1≥0\\ x-y-1≤0\\ x-3y+3≥0\end{array}\right.$,则z=x+3y的最大值为9.分析 先由约束条件画出可行域,再求出可行域各个角点的坐标,将坐标逐一代入目标函数,验证即得答案.
解答  解:如图即为满足约束条件$\left\{\begin{array}{l}x+y-1≥0\\ x-y-1≤0\\ x-3y+3≥0\end{array}\right.$的可行域,
解:如图即为满足约束条件$\left\{\begin{array}{l}x+y-1≥0\\ x-y-1≤0\\ x-3y+3≥0\end{array}\right.$的可行域,
由图易得:由$\left\{\begin{array}{l}{x-y-1=0}\\{x-3y+3=0}\end{array}\right.$,解得B(3,2),同理可得A(0,1),C(1,0),当x=3,y=2时
z=x+3y的最大值为9,
故答案为:9.
点评 在解决线性规划的小题时,我们常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.

练习册系列答案
相关题目
18.设函数f(x)=$\left\{\begin{array}{l}{{e}^{x},0≤x<1}\\{lnx+e,1≤x≤e}\end{array}\right.$在区间[0,e]上随机取一个实数x,则f(x)的值不小于常数e的概率是( )
| A. | $\frac{1}{e}$ | B. | 1-$\frac{1}{e}$ | C. | $\frac{e}{1+e}$ | D. | $\frac{1}{1+e}$ |
19.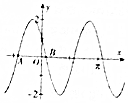 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,其中A(-$\frac{5π}{12}$,0),B($\frac{π}{12}$,0),则函数f(x)的单调增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,其中A(-$\frac{5π}{12}$,0),B($\frac{π}{12}$,0),则函数f(x)的单调增区间为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,其中A(-$\frac{5π}{12}$,0),B($\frac{π}{12}$,0),则函数f(x)的单调增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,其中A(-$\frac{5π}{12}$,0),B($\frac{π}{12}$,0),则函数f(x)的单调增区间为( )| A. | [-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z) | B. | [$\frac{π}{3}$+kπ,$\frac{5π}{6}$+kπ](k∈Z) | ||
| C. | [-$\frac{π}{6}$+2kπ,$\frac{π}{3}$+2kπ](k∈Z) | D. | [$\frac{π}{3}$+2kπ,$\frac{5π}{6}$+2kπ](k∈Z) |
3.已知集合A={x|x=3n+2,n∈N},B={6,8,10,12,14},则集合A∩B=( )
| A. | {8,10} | B. | {8,12} | C. | {8,14} | D. | {8,10,14} |
13.某企业为了对生产的一种新产品进行合理定价,将该产品按事先拟定的价格进行试销,得到以下数据:
(Ⅰ)画出散点图,并求y关于x的回归方程;
(Ⅱ)已知该产品的成本是36元/件,预计在今后的销售中,销量与单价仍然服从(Ⅰ)中的关系,为使企业获得最大利润,该产品的单价应定为多少元(精确到元)?
附:回归直线$\stackrel{∧}{y}$=$\stackrel{∧}{a}$+$\stackrel{∧}{b}$x的斜率和截距的最小二乘法估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{(x}_{i}-\overline{x}){(y}_{i}-\overline{y})}{{\sum_{i=1}^{n}{(x}_{i}-\overline{x})}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
| 销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
(Ⅱ)已知该产品的成本是36元/件,预计在今后的销售中,销量与单价仍然服从(Ⅰ)中的关系,为使企业获得最大利润,该产品的单价应定为多少元(精确到元)?
附:回归直线$\stackrel{∧}{y}$=$\stackrel{∧}{a}$+$\stackrel{∧}{b}$x的斜率和截距的最小二乘法估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{(x}_{i}-\overline{x}){(y}_{i}-\overline{y})}{{\sum_{i=1}^{n}{(x}_{i}-\overline{x})}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
18.已知双曲线C:$\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率e=$\frac{\sqrt{5}}{2}$,点P是抛物线y2=4x上的一个动点,P到双曲线C的上焦点F1(0,c)的距离与到直线x=-1的距离之和的最小值为$\sqrt{6}$,则该双曲线的方程为( )
| A. | $\frac{{y}^{2}}{2}-\frac{{x}^{2}}{3}$=1 | B. | y2-$\frac{{x}^{2}}{4}$=1 | C. | $\frac{{y}^{2}}{4}$-x2=1 | D. | $\frac{{y}^{2}}{3}-\frac{{x}^{2}}{2}$=1 |
 如甲图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起到△D1AE位置,使平面D1AE⊥平面ABCE,得到乙图所示的四棱锥D1-ABCE.
如甲图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起到△D1AE位置,使平面D1AE⊥平面ABCE,得到乙图所示的四棱锥D1-ABCE.