题目内容
已知
为单调递增的等比数列，且
，
，
是首项为2，公差为
的等差数列，其前
项和为
.
（Ⅰ）求数列的通项公式；
（Ⅱ）当且仅当
，
，
成立，求的取值范围.
解：（Ⅰ）因为为等比数列，所以 
所以 
所以 
为方程 
的两根；
又因为为递增的等比数列， 所以 
从而
，
所以 
；
（Ⅱ）由题意可知：
，
，
由已知可得：
，
所以 
，
当且仅当，且时，上式成立，
设
，则
，
所以
，
所以 的取值范围为
.
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
＝ ；
中，三边长
满足
，那么
中，
分别为角
的对边，若
，且
，则
．
上一动点M，与直线
，则M到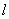
的最短距离是 。