题目内容
17.若一个复数的实部与虚部互为相反数,则称此复数为“理想复数”.已知z=$\frac{a}{1-2i}$+bi(a,b∈R)为“理想复数”,则( )| A. | a-5b=0 | B. | 3a-5b=0 | C. | a+5b=0 | D. | 3a+5b=0 |
分析 利用复数代数形式的乘除运算化简,结合已知得答案.
解答 解:∵z=$\frac{a}{1-2i}$+bi=$\frac{a(1+2i)}{(1-2i)(1+2i)}+bi=\frac{a}{5}+(\frac{2a}{5}+b)i$.
由题意,$\frac{a}{5}=-\frac{2a}{5}-b$,则3a+5b=0.
故选:D.
点评 本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
11.已知F是双曲线C:y2-mx2=3m(m>0)的一个焦点,则点F到C的一条渐近线的距离为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
12. 某程序框图如图所示,其中t∈Z,该程序运行后输出的k=2,则t的最大值为( )
某程序框图如图所示,其中t∈Z,该程序运行后输出的k=2,则t的最大值为( )
 某程序框图如图所示,其中t∈Z,该程序运行后输出的k=2,则t的最大值为( )
某程序框图如图所示,其中t∈Z,该程序运行后输出的k=2,则t的最大值为( )| A. | 11 | B. | 2057 | C. | 2058 | D. | 2059 |
2.若直线y=x+b与圆x2+y2=1有公共点,则实数b的取值范围是( )
| A. | [-1,1] | B. | [0,1] | C. | [0,$\sqrt{2}$] | D. | [-$\sqrt{2}$,$\sqrt{2}$] |
9.已知F1和F2分别是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左焦点和右焦点,点P(x0,y0)是椭圆C上一点,切满足∠F1PF2≥60°,则x0的取值范围是( )
| A. | [-1,1] | B. | [-$\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$] | C. | [1,$\sqrt{2}$] | D. | [$\frac{2\sqrt{3}}{3}$,$\sqrt{2}$] |
6.已知F1(-c,0),F2(c,0)为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的两个焦点,点P(不在x轴上)为椭圆上的一点,且满足${\overrightarrow{PF}_1}•\overrightarrow{P{F_2}}={c^2}$,则椭圆的离心率的取值范围是( )
| A. | $[{\frac{{\sqrt{3}}}{3},1})$ | B. | $[{\frac{1}{3},\frac{1}{2}}]$ | C. | $[{\frac{{\sqrt{3}}}{3},\frac{{\sqrt{2}}}{2}})$ | D. | $({0,\frac{{\sqrt{2}}}{2}}]$ |
 值是( )
值是( )
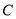 :
: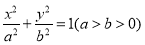 的左焦点为
的左焦点为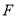 ,
, 为椭圆上一点,
为椭圆上一点,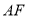 交
交 轴于点
轴于点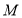 ,且
,且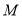 为
为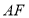 的中点.
的中点.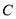 的方程;
的方程;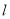 与椭圆
与椭圆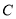 有且只有一个公共点
有且只有一个公共点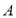 ,平行于
,平行于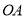 的直线交
的直线交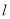 于
于 ,交椭圆
,交椭圆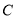 于不同的亮点
于不同的亮点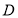 ,
,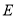 ,问是否存在常熟
,问是否存在常熟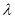 ,使得
,使得 ,若存在,求出
,若存在,求出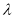 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.