题目内容
已知f(x)=x+asinx.
(Ⅰ) 若a=2,求f(x)在[0,π]上的单调递减区间;
(Ⅱ)若f(x)在(-∞,+∞)上为增函数,求实数a的取值范围;
(Ⅲ)当常数a≠0时,设g(x)= ,求g(x)在
,求g(x)在 上的最值.
上的最值.
解:(Ⅰ) 当a=2时,f(x)=x+2sinx所以f'(x)=1+2cosx….….(1分)
当f'(x)<0时, ….….(2分)
….….(2分)
所以 f(x)在[0,π]上的单调递减区间为 ….….(4分)
….….(4分)
(Ⅱ)∵f(x)在(-∞,+∞)上为增函数,
∴f'(x)=1+acosx≥0对x∈(-∞,+∞)恒立. …(5分)
法一:令t=cosx,则1+at≥0对t∈[-1,1]恒成立,…(7分)
∴ ,解得-1≤a≤1,
,解得-1≤a≤1,
∴实数a的取值范围是[-1,1]. …(9分)
法二:当cosx>0时, ,即
,即 ,所以a≥-1…(6分)
,所以a≥-1…(6分)
当cosx<0时, ,即
,即 ,所以a≤1…(7分)
,所以a≤1…(7分)
当cosx=0时,f(x)=1≥0恒成立,所以a∈R…(8分)
综上所述,实数a的取值范围是[-1,1]. …(9分)
(Ⅲ)g(x)= ,∴g′(x)=
,∴g′(x)= ,…(10分)
,…(10分)
记h(x)=xcosx-sinx,x∈(0,π),
则h′(x)=-xsinx<0对x∈(0,π)恒成立,…(11分)
∴h(x)在x∈(0,π)上是减函数,
∴h(x)<h(0),即g′(x)<0,…(12分)
①当a>0时,g(x)= 在(0,π)上是减函数,
在(0,π)上是减函数,
得g(x)在 上为减函数.
上为减函数.
∴当x= 时,g(x)取得最大值1+
时,g(x)取得最大值1+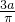 ;当x=
;当x= 时,
时,
g(x)取得最小值1+ .…(13分)
.…(13分)
②当a<0时,g(x)= 在(0,π)上是增函数,
在(0,π)上是增函数,
得g(x)在 上为增函数.
上为增函数.
∴当x= 时,g(x)取得最大值1+
时,g(x)取得最大值1+ ;
;
当x= 时,g(x)取得最小值1+
时,g(x)取得最小值1+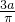 .…(14分)
.…(14分)
分析:(Ⅰ)把a=2代入f(x),然后对f(x)进行求导,可以令f′(x)<0,解出x的范围即可;
(Ⅱ)根据f(x)在(-∞,+∞)上为增函数,结合导数得到f'(x)=1+acosx≥0对x∈(-∞,+∞)恒立.
法一:利用换元法,令t=cosx,则1+at≥0对t∈[-1,1]恒成立,利用一次函数的性质得出关于a的不等关系即可求出实数a的取值范围;
法二:分类讨论法,对cosx的正负进行分类讨论:当cosx>0时, ,即
,即 ;当cosx<0时,
;当cosx<0时, ,即
,即 ;当cosx=0时,f(x)=1≥0恒成立,综上所述,可得实数a的取值范围.
;当cosx=0时,f(x)=1≥0恒成立,综上所述,可得实数a的取值范围.
(Ⅲ)常数a≠0时,设g(x)= ,利用求导法则,对g(x)进行求导,求出x在[0,π]上的极值点,利用导数研究其最值问题.
,利用求导法则,对g(x)进行求导,求出x在[0,π]上的极值点,利用导数研究其最值问题.
点评:此题主要考查利用导数研究函数的单调性和最值问题,解题的关键是能够对g(x)进行正确求导,此题是一道中档题.
当f'(x)<0时,
 ….….(2分)
….….(2分)所以 f(x)在[0,π]上的单调递减区间为
 ….….(4分)
….….(4分)(Ⅱ)∵f(x)在(-∞,+∞)上为增函数,
∴f'(x)=1+acosx≥0对x∈(-∞,+∞)恒立. …(5分)
法一:令t=cosx,则1+at≥0对t∈[-1,1]恒成立,…(7分)
∴
 ,解得-1≤a≤1,
,解得-1≤a≤1,∴实数a的取值范围是[-1,1]. …(9分)
法二:当cosx>0时,
 ,即
,即 ,所以a≥-1…(6分)
,所以a≥-1…(6分)当cosx<0时,
 ,即
,即 ,所以a≤1…(7分)
,所以a≤1…(7分)当cosx=0时,f(x)=1≥0恒成立,所以a∈R…(8分)
综上所述,实数a的取值范围是[-1,1]. …(9分)
(Ⅲ)g(x)=
 ,∴g′(x)=
,∴g′(x)= ,…(10分)
,…(10分)记h(x)=xcosx-sinx,x∈(0,π),
则h′(x)=-xsinx<0对x∈(0,π)恒成立,…(11分)
∴h(x)在x∈(0,π)上是减函数,
∴h(x)<h(0),即g′(x)<0,…(12分)
①当a>0时,g(x)=
 在(0,π)上是减函数,
在(0,π)上是减函数,得g(x)在
 上为减函数.
上为减函数.∴当x=
 时,g(x)取得最大值1+
时,g(x)取得最大值1+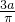 ;当x=
;当x= 时,
时,g(x)取得最小值1+
 .…(13分)
.…(13分)②当a<0时,g(x)=
 在(0,π)上是增函数,
在(0,π)上是增函数,得g(x)在
 上为增函数.
上为增函数.∴当x=
 时,g(x)取得最大值1+
时,g(x)取得最大值1+ ;
;当x=
 时,g(x)取得最小值1+
时,g(x)取得最小值1+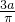 .…(14分)
.…(14分)分析:(Ⅰ)把a=2代入f(x),然后对f(x)进行求导,可以令f′(x)<0,解出x的范围即可;
(Ⅱ)根据f(x)在(-∞,+∞)上为增函数,结合导数得到f'(x)=1+acosx≥0对x∈(-∞,+∞)恒立.
法一:利用换元法,令t=cosx,则1+at≥0对t∈[-1,1]恒成立,利用一次函数的性质得出关于a的不等关系即可求出实数a的取值范围;
法二:分类讨论法,对cosx的正负进行分类讨论:当cosx>0时,
 ,即
,即 ;当cosx<0时,
;当cosx<0时, ,即
,即 ;当cosx=0时,f(x)=1≥0恒成立,综上所述,可得实数a的取值范围.
;当cosx=0时,f(x)=1≥0恒成立,综上所述,可得实数a的取值范围.(Ⅲ)常数a≠0时,设g(x)=
 ,利用求导法则,对g(x)进行求导,求出x在[0,π]上的极值点,利用导数研究其最值问题.
,利用求导法则,对g(x)进行求导,求出x在[0,π]上的极值点,利用导数研究其最值问题.点评:此题主要考查利用导数研究函数的单调性和最值问题,解题的关键是能够对g(x)进行正确求导,此题是一道中档题.

练习册系列答案
相关题目
 ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由. ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由.