题目内容
3.已知命题p:方程$\frac{{x}^{2}}{m-2}$+$\frac{{y}^{2}}{4-m}$=1表示焦点在y轴上的椭圆;命题q:方程$\frac{{x}^{2}}{3-m}$+$\frac{{y}^{2}}{m}$=1表示双曲线;若p∨q为真,p∧q为假,求实数m的取值范围.分析 由p∨q为真,p∧q为假可得命题p与命题q一真一假,分别求出p、q为真及假时的m的范围,取交集后再取并集得答案.
解答 解:由题意知:命题p与命题q一真一假,
p为真命题:4-m>m-2>0,解得2<m<3,
q为真命题:(3-m)m<0,解得m<0或m>3,
若p真q假,则2<m<3,
若p假q真:m<0或m>3,
综上:m<0或2<m<3或m>3.
点评 本题考查复合命题的真假判断,考查了椭圆与双曲线的标准方程,是中档题.

练习册系列答案
相关题目
13.已知一个三棱锥的三视图如图所示,若该三棱锥的四个顶点均在同一球面上,则该求的体积为( )
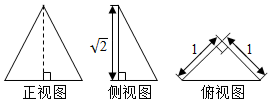

| A. | $\frac{32π}{3}$ | B. | 4π | C. | 2π | D. | $\frac{4π}{3}$ |
11.设a,b∈R,那么“${π^{\frac{a}{b}}}>π$”是“ea>eb>1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.命题“?x∈R,使得x2<1”的否定是( )
| A. | ?x∈R,都有x2<1 | B. | ?x∈R,使得x2>1 | ||
| C. | ?x∈R,使得x2≥1 | D. | ?x∈R,都有x≤-1或x≥1 |
13.已知直线y=kx是曲线y=3x的切线,则k的值是( )
| A. | $\frac{1}{3}$ | B. | eln3 | C. | log3e | D. | e |
