题目内容
△ABC中,AB=2| 2 |
| 5 |
| 1 |
| 2 |
分析:先根据题意和余弦定理,在△ABC中求出AC的长,再求出AD的长,再由余弦定理在△ABD中求出BD的长.
解答:解:设AC=x,由余弦定理得,BC2=AB2+AC2-2AB•ACcosA,
5=8+x2-2×2
×x×
,即x2-4x+3=0,解得x=1或3,
∵∠B为△ABC中最大角,∴x=3,又∵AD=
DC,∴AD=1,
在△ABD中,由余弦定理得,
BD2=AB2+AD2-2AB•ADcosA=8+1-2×2
×1×
=5,
∴BD=
,
故答案为:
.
5=8+x2-2×2
| 2 |
| ||
| 2 |
∵∠B为△ABC中最大角,∴x=3,又∵AD=
| 1 |
| 2 |
在△ABD中,由余弦定理得,
BD2=AB2+AD2-2AB•ADcosA=8+1-2×2
| 2 |
| ||
| 2 |
∴BD=
| 5 |
故答案为:
| 5 |
点评:本题主要考查了利用余弦定理解三角形,根据题意需要利用不同的三角形进行求解,注意选择适当的定理去求解.

练习册系列答案
相关题目
 如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC=
如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC=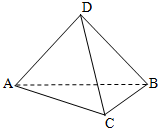 如图,A、B、C、D是空间四点,在△ABC中,AB=2,AC=BC=
如图,A、B、C、D是空间四点,在△ABC中,AB=2,AC=BC=