题目内容
（2012•湖南）在△ABC中，AB=2，AC=3，
•
=1，则BC=（ ）
| AB |
| BC |
分析：设∠B=θ，由
•
=1，利用平面向量的数量积运算法则列出关系式，表示出cosθ，再利用余弦定理表示出cosθ，两者相等列出关于BC的方程，求出方程的解即可得到BC的长．
| AB |
| BC |
解答：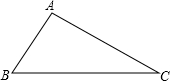
解：根据题意画出相应的图形，如图所示：
∵
•
=1，设∠B=θ，AB=2，
∴2•BC•cos（π-θ）=1，即cosθ=-
，
又根据余弦定理得：cosθ=
=
，
∴-
=
，即BC2=3，
则BC=
．
故选A
解：根据题意画出相应的图形，如图所示：∵
| AB |
| BC |
∴2•BC•cos（π-θ）=1，即cosθ=-
| 1 |
| 2BC |
又根据余弦定理得：cosθ=
| 22+BC2-32 |
| 4BC |
| BC2-5 |
| 4BC |
∴-
| 1 |
| 2BC |
| BC2-5 |
| 4BC |
则BC=
| 3 |
故选A
点评：此题属于解三角形的题型，涉及的知识有：平面向量的数量积运算，余弦定理，以及诱导公式的运用，熟练掌握定理及法则是解本题的关键．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目