题目内容
在等腰△ABC中,AB=AC,若AC边上的中线BD的长为6,则△ABC的面积的最大值是 .
分析:设AB=AC=2x,三角形的顶角θ,则由余弦定理求得cosθ的表达式,进而根据同角三角函数基本关系求得sinθ,最后根据三角形面积公式表示出三角形面积的表达式,根据一元二次函数的性质求得面积的最大值.
解答: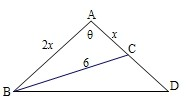 解:设AB=AC=2x,AC=x.
解:设AB=AC=2x,AC=x.
设三角形的顶角θ,则由余弦定理得cosθ=
=
,
∴sinθ=
=
=
=
=
=
=
,
根据公式三角形面积S=
absinθ=
×2x•2x•
=
,
∴当 x2=20时,三角形面积有最大值
=
=
×48=24.
故答案为:24
 解:设AB=AC=2x,AC=x.
解:设AB=AC=2x,AC=x.设三角形的顶角θ,则由余弦定理得cosθ=
| (2x)2+x2-36 |
| 2×2x•x |
| 5x2-36 |
| 4x2 |
∴sinθ=
| 1-cos2θ |
1-(
|
|
| ||
| 4x2 |
| ||
| 4x2 |
=
| ||
| 4x2 |
| ||
| 4x2 |
根据公式三角形面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4x2 |
| 1 |
| 2 |
| -9(x2-20)2+602-362 |
∴当 x2=20时,三角形面积有最大值
| 1 |
| 2 |
| 602-362 |
| 1 |
| 2 |
| 96×24 |
| 1 |
| 2 |
故答案为:24
点评:本题主要考查函数最值的应用,根据条件设出变量,根据三角形的面积公式以及三角函数的关系是解决本题的关键,利用二次函数的性质即可求出函数的最值,考查学生的运算能力.运算量较大.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
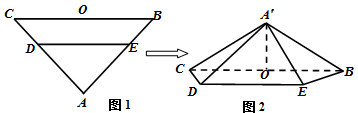
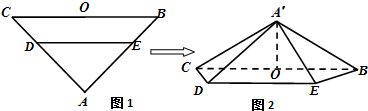 如图1,在等腰△ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,
如图1,在等腰△ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,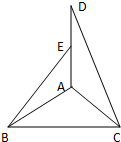 如图,在等腰△ABC中,
如图,在等腰△ABC中, 如图,在等腰△ABC中,AB=AC=1,∠B=30°,则向量
如图,在等腰△ABC中,AB=AC=1,∠B=30°,则向量