题目内容
7.解下列不等式(组),用区间表示(1)$\left\{\begin{array}{l}{3x-9<-7}\\{9-3x≥4}\end{array}\right.$
(2)(x+1)(2x-3)<0.
分析 (1)分别求出不等式的解,取交集即可;(2)解不等式求出不等式的解集即可.
解答 解:(1)解3x-9<-7得:x<$\frac{2}{3}$,
解9-3x≥4得:x≤$\frac{5}{3}$,
故不等式的解集是:(-∞,$\frac{2}{3}$);
(2)∵(x+1)(2x-3)<0,
∴-1<x<$\frac{3}{2}$,
∴不等式的解集是:(-1,$\frac{3}{2}$).
点评 本题考察了求不等式的解集问题,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列判断错误的是( )
| A. | “am2<bm2”是“a<b”的充分不必要条件 | |
| B. | 命题“?x∈R,x3-x2≤0”的否定是“?x∈R,x3-x2-1>0” | |
| C. | “若a=1,则直线x+y=0和直线x-ay=0互相垂直”的逆否命题为真命题 | |
| D. | 若p∧q为假命题,则p,q均为假命题 |
19.下列有关命题的叙述错误的是( )
| A. | 若非p是q的必要条件,则p是非q的充分条件 | |
| B. | “x>2”是“$\frac{1}{x}<\frac{1}{2}$”的充分不必要条件 | |
| C. | 命题“?x∈R,x2-x≥0”的否定是“?x∈R,x2-x<0” | |
| D. | 若p且q为假命题,则p,q均为假命题 |
16.已知复数z,“z+$\overline{z}$=0”是“z为纯虚数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也不必要条件 |
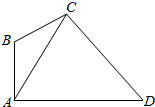 在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.
在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.