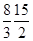题目内容
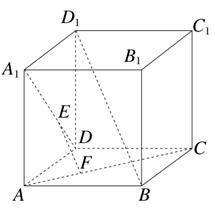
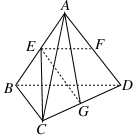
如图,正方体ABCD-A1B1C1D1中,E,F分别在A1D,AC上,且A1E=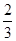 A1D,AF=
A1D,AF=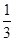 AC,则( )
AC,则( )
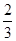 A1D,AF=
A1D,AF=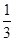 AC,则( )
AC,则( )
| A.EF至多与A1D,AC之一垂直 |
| B.EF⊥A1D,EF⊥AC |
| C.EF与BD1相交 |
| D.EF与BD1异面 |
B
以D点为坐标原点,以DA,DC,DD1所在直线分别为x,y,z轴建立空间直角坐标系,设正方体棱长为1,则A1(1,0,1),D(0,0,0),A(1,0,0),C(0,1,0),E(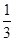 ,0,
,0,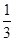 ),F(
),F(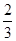 ,
,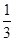 ,0),B(1,1,0),D1(0,0,1),
,0),B(1,1,0),D1(0,0,1),
 =(-1,0,-1),
=(-1,0,-1), =(-1,1,0),
=(-1,1,0),
 =(
=(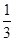 ,
,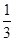 ,-
,-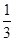 ),
), =(-1,-1,1),
=(-1,-1,1),
 =-
=-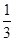
 ,
, ·
· =
= ·
· =0,
=0,
从而EF∥BD1,EF⊥A1D,EF⊥AC.故选B.
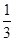 ,0,
,0,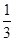 ),F(
),F(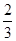 ,
,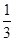 ,0),B(1,1,0),D1(0,0,1),
,0),B(1,1,0),D1(0,0,1), =(-1,0,-1),
=(-1,0,-1), =(-1,1,0),
=(-1,1,0), =(
=(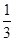 ,
,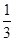 ,-
,-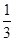 ),
), =(-1,-1,1),
=(-1,-1,1), =-
=-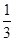
 ,
, ·
· =
= ·
· =0,
=0,从而EF∥BD1,EF⊥A1D,EF⊥AC.故选B.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
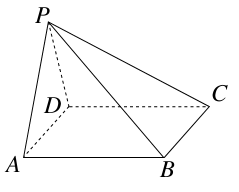
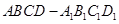 的所有棱长都相等,
的所有棱长都相等,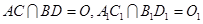 ,四边形
,四边形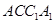 和四边形
和四边形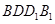 为矩形.
为矩形.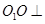 底面
底面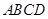 ;
; ,求二面角
,求二面角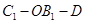 的余弦值.
的余弦值.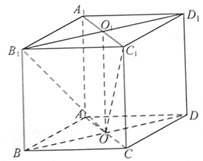
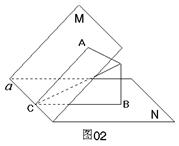
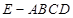 中,平面
中,平面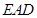
 平面
平面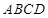 ,
,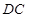 //
//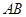 ,
,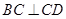 ,
,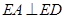 ,且
,且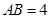 ,
,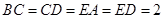 .
.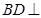 平面
平面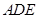 ;
;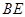 和平面
和平面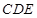 所成角的正弦值;
所成角的正弦值; 上是否存在一点
上是否存在一点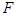 使得平面
使得平面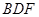
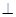 平面
平面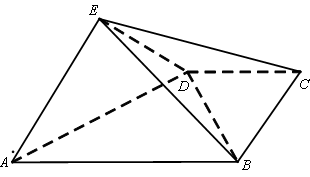
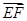 ·
·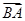 ;
;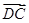 ;
;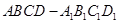 中
中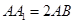 ,则
,则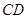 与平面
与平面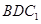 所成角的正弦值等于( )
所成角的正弦值等于( )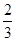
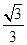
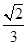
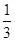
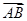 =(2,4,5),
=(2,4,5),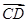 =(3,x,y),若
=(3,x,y),若