题目内容
4．函数f（x）=$\frac{1}{-2{x}^{2}-3x-5}$的最小值为-$\frac{8}{31}$．分析 利用配方法可得-2x2-3x-5=-2（x-$\frac{3}{4}$）2-$\frac{31}{8}$，从而求函数的最值．
解答 解：∵-2x2-3x-5=-2（x-$\frac{3}{4}$）2-$\frac{31}{8}$，
∴-2x2-3x-5≤-$\frac{31}{8}$，
∴$\frac{1}{-2{x}^{2}-3x-5}$≥-$\frac{8}{31}$，
故函数f（x）=$\frac{1}{-2{x}^{2}-3x-5}$的最小值为-$\frac{8}{31}$，
故答案为：-$\frac{8}{31}$．
点评 本题考查了函数的最值的求法，利用了配方法．
练习册系列答案
相关题目
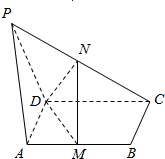如图，PA⊥平面ABCD，ABCD是矩形，M、N分别是AB，PC的中点．
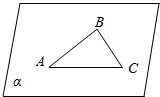如图，在△ABC中，若AB，BC在平面α内，试判断AC是否在平面α内．