题目内容
已知a∈R,求函数f(x)=(2-3a)x2-2x+a在区间[0,1]上的最小值.
解:Ⅰ、当2-3a=0,即 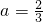 时,
时,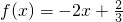 在[0,1]上递减
在[0,1]上递减
∴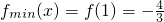 (2分)
(2分)
当2-3a≠0,即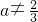 时,f(x)为二次函数 (3分)
时,f(x)为二次函数 (3分)
Ⅱ、若2-3a>0,即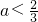 时,f(x)的开口向上,其对称轴为
时,f(x)的开口向上,其对称轴为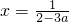 (4分)
(4分)
①当2-3a>1时,即 时,此时
时,此时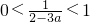 ,
,
∴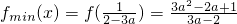 (6分)
(6分)
②当 0<2-3a≤1,即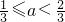 时,此时
时,此时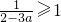 ,fmin(x)=f(1)=-2a (8分)
,fmin(x)=f(1)=-2a (8分)
Ⅲ、若2-3a<0,即a 时,f(x)的开口向下,其对称轴为
时,f(x)的开口向下,其对称轴为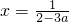 (9分)
(9分)
fmin(x)=f(1)=-2a (10分)
综上可得: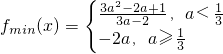 (12分)
(12分)
分析:先对二次项系数进行分类讨论,再考虑二次函数的对称轴与区间的位置关系,从而确定函数f(x)=(2-3a)x2-2x+a在区间[0,1]上的最小值.
点评:本题重点考查函数在指定区间上的最值,考查分类讨论的数学思想,解题的关键是掌握二次函数求最值的方法.
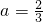 时,
时,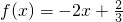 在[0,1]上递减
在[0,1]上递减∴
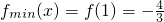 (2分)
(2分)当2-3a≠0,即
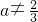 时,f(x)为二次函数 (3分)
时,f(x)为二次函数 (3分)Ⅱ、若2-3a>0,即
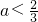 时,f(x)的开口向上,其对称轴为
时,f(x)的开口向上,其对称轴为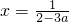 (4分)
(4分)①当2-3a>1时,即
 时,此时
时,此时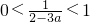 ,
,∴
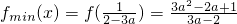 (6分)
(6分)②当 0<2-3a≤1,即
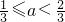 时,此时
时,此时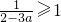 ,fmin(x)=f(1)=-2a (8分)
,fmin(x)=f(1)=-2a (8分)Ⅲ、若2-3a<0,即a
 时,f(x)的开口向下,其对称轴为
时,f(x)的开口向下,其对称轴为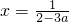 (9分)
(9分)fmin(x)=f(1)=-2a (10分)
综上可得:
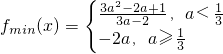 (12分)
(12分)分析:先对二次项系数进行分类讨论,再考虑二次函数的对称轴与区间的位置关系,从而确定函数f(x)=(2-3a)x2-2x+a在区间[0,1]上的最小值.
点评:本题重点考查函数在指定区间上的最值,考查分类讨论的数学思想,解题的关键是掌握二次函数求最值的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目