题目内容
图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.从这个茎叶图可以看出甲、乙两名运动员得分的中位数分别是( )
| A.31,26 | B.36,23 |
| C.36,26 | D.31,23 |
C
解析试题分析:根据已知中的茎叶图数据可知,对于甲而言,共有13个数据,那么最中间的数据为第7个,从小到大得到,即为36.而对于乙,一共有数据11个,也是奇数个数据,那么最中间的为第6个数,业绩是26,这样可以选C.
考点:本试题考查了茎叶图的知识。
点评:解决这个问题的关键是对于中位数概念的理解,就是将数据从小到大排列好,则最中间的一个数或者是最中间两个数的平均值即为所求,属于基础题。

 特高级教师点拨系列答案
特高级教师点拨系列答案以下有关线性回归分析的说法不正确的是
A.通过最小二乘法得到的线性回归直线经过样本的中心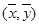 |
B.用最小二乘法求回归直线方程,是寻求使 最小的a,b的值 最小的a,b的值 |
| C.相关系数r越小,表明两个变量相关性越弱 |
D. 越接近1,表明回归的效果越好 越接近1,表明回归的效果越好 |
某校为了研究学生的性别和对待某一活动的态度(支持和不支持两种态度)的关系,运用 列联表进行独立性检验,经计算
列联表进行独立性检验,经计算 ,则所得到的统计学结论是:有( )的把握认为“学生性别与支持该活动有关系”。
,则所得到的统计学结论是:有( )的把握认为“学生性别与支持该活动有关系”。
 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
某校从参加高二年级学业水平测试的学生中抽出100名学生,其数学成绩的频率分布直方图如图所示.其中 成绩分组区间是[40,50),[50,60),[60,70),[70,80), [80,90) ,[90,100].则成绩在[80 ,100]上的人数为
| A.70 |
| B.60 |
| C.35 |
| D.30 |
下列命题正确的有
①用相关指数 来刻画回归效果,
来刻画回归效果, 越小,说明模型的拟合效果越好;
越小,说明模型的拟合效果越好;
②命题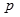 :“
:“ ”的否定
”的否定 :“
:“ ”;
”;
③设随机变量 服从正态分布
服从正态分布 , 若
, 若 ,则
,则 ;
;
④回归直线一定过样本中心( ).
).
| A.1个 | B.2个 | C.3个 | D.4个 |
一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归模型为y=7.19x+73.93,用这个模型预测这个孩子10岁时的身高,则正确的叙述是( )
| A.身高一定是145.83cm | B.身高在145.83cm以上 |
| C.身高在145.83cm以下 | D.身高在145.83cm左右 |
某单位有老年人28 人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为36样本,则老年人、中年人、青年人分别各抽取的人数是( )
| A.6, 12 ,18 | B.7,11,19 |
| C.6,13,17 | D.7,12,17 |
 和
和 ,样本标准差分别为
,样本标准差分别为 和
和 ,则( )
,则( )




 人,中级管理人员
人,中级管理人员 人,高级管理人员
人,高级管理人员 人,要从其中抽取
人,要从其中抽取 个人进行身体健康检查,如果采用分层抽样的方法,其中高级管理人员仅抽到1人,那么
个人进行身体健康检查,如果采用分层抽样的方法,其中高级管理人员仅抽到1人,那么