题目内容
下列命题正确的有
①用相关指数 来刻画回归效果,
来刻画回归效果, 越小,说明模型的拟合效果越好;
越小,说明模型的拟合效果越好;
②命题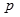 :“
:“ ”的否定
”的否定 :“
:“ ”;
”;
③设随机变量 服从正态分布
服从正态分布 , 若
, 若 ,则
,则 ;
;
④回归直线一定过样本中心( ).
).
| A.1个 | B.2个 | C.3个 | D.4个 |
C
解析试题分析:①R2越大拟合效果越好,故①不正确;
②由存在性命题的否定是全称命题得②正确;
③正态分布函数曲线的特点是:关于x=0对称,在x=0处达到最大值,且p(ξ<0)= ,若P(ξ>1)=p则若P(ξ<﹣1)=p,所以
,若P(ξ>1)=p则若P(ξ<﹣1)=p,所以 .故③正确;
.故③正确;
④样本中心点在直线上,故④正确。
故选C.
考点:本题主要考查命题的真假判断。
点评:小综合题,命题涉及知识面较广,因此在判断命题真假过程中,要综合应用所学知识。

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
我校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一、高二、高三各年级抽取的人数分别为( )
| A.45,75,15 | B.45,45,45 |
| C.30,90,15 | D.45,60,30 |
在对两个变量x、y进行线性回归分析时一般有下列步骤:
①对所求出的回归方程作出解释;
②收集数据 [
[
③求线性回归方程;
④求相关系数;
⑤根据所搜集的数据绘制散点图.
若根据实际情况能够判定变量x、y具有线性相关性,则在下列操作顺序中正确的是
| A.①②⑤③④ | B.③②④⑤① | C.②④③①⑤ | D.②⑤④③① |
某中学从已编号(1~60)的60个班级中,随机抽取6个班级进行卫生检查,用每部分选取的号码间隔一样的系统抽样方法确定所选的6个班级的编号可能是( )
| A.6,16,26,36,46,56 | B.3,10,17,24,31,38 |
| C.4,11,18,25,32,39 | D.5,14,23,32,41,50 |
图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.从这个茎叶图可以看出甲、乙两名运动员得分的中位数分别是( )
| A.31,26 | B.36,23 |
| C.36,26 | D.31,23 |
在如图所示的“茎叶图”表示的数据中,众数和中位数分别是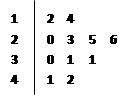
| A.23与26 | B.31与26 |
| C.24与30 | D.26与30 |
某样本数据的频率分布直方图的部分图形如右图所示,则数据在[50,70)的频率约为( )
| A.0.25 | B.0.05 | C.0.5 | D.0.025 |

 ,
,
 、
、 取值如下表:
取值如下表: ,则
,则
 B.
B.  C.
C.  D.
D. 