题目内容
如图:样本A和B分别取自两个不同的总体,他们的样本平均数分别为 和
和 ,样本标准差分别为
,样本标准差分别为 和
和 ,则( )
,则( )
A. |
B. |
C. |
D. |
B
解析试题分析:由图易知 ,因为A中的数据较为分散,B中的数据较为集中,所以
,因为A中的数据较为分散,B中的数据较为集中,所以 ,因此选B。
,因此选B。
考点:平均数的概念;标准差的概念。
点评:标准差是用来衡量数据分散程度的量,数据越集中,标准差越小,数据越分散,标准差越大。

练习册系列答案
相关题目
在如下图所示的各图中,两个变量具有相关关系的是( )
| A.(1)(2) | B.(1)(3) |
| C.(2)(4) | D.(2)(3) |
对变量 有观测数据
有观测数据 …,10),得散点图(1)所示.对变量
…,10),得散点图(1)所示.对变量 有观测数据
有观测数据 ,…,10),得散点图(2).由这两个散点图可以判断
,…,10),得散点图(2).由这两个散点图可以判断
A.变量 与 与 正相关, 正相关,  与 与 正相关 正相关 | B.变量 与 与 正相关, 正相关,  与 与 负相关 负相关 |
C.变量 与 与 负相关, 负相关,  与 与 正相关 正相关 | D.变量 与 与 负相关, 负相关,  与 与 负相关 负相关 |
图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.从这个茎叶图可以看出甲、乙两名运动员得分的中位数分别是( )
| A.31,26 | B.36,23 |
| C.36,26 | D.31,23 |
为调查参加运动会的1000名运动员的年龄情况,从中抽查了100名运动员的年龄作为样
本,就这个问题来说,下列说法正确的是( )
| A.1000名运动员是总体 | B.每个运动员是个体 |
| C.抽取的100名运动员的年龄是样本 | D.样本容量是1000 |
如图是歌手大奖赛中,七位评委给甲、乙两名选手打出的分数的茎叶图(其中m为0~9中的一个正整数),现将甲、乙所得的一个最高分和一个最低分均去掉后,甲、乙两名选手得分的平均数分别为 ,中位数分别为
,中位数分别为 ,则有( )
,则有( )
A. , ,  , , | B. , ,  |
C. , ,  , , | D. 与 与 大小均不能确定 大小均不能确定 |
 的人做问卷
的人做问卷 ,编号落入间
,编号落入间 的人做问卷
的人做问卷 ,其余的人做问卷
,其余的人做问卷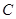 .则抽到的人中,做问卷
.则抽到的人中,做问卷 分钟抽取一件产品进行某项指标的检测 ,这样的抽样是分层抽样;
分钟抽取一件产品进行某项指标的检测 ,这样的抽样是分层抽样; 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好; 中,当解释变量
中,当解释变量 每增加一个单位时,预报变量
每增加一个单位时,预报变量 平均增加
平均增加 个单位;
个单位; 与
与 ,若它们的随机变量
,若它们的随机变量 的观测值
的观测值 越小,则判断“
越小,则判断“