题目内容
8.空气污染指数划分为0-50(优),51-100(良),101-150(轻度污染),151-200(中度污染),201-300(重度污染)和大于300(严重污染)六档,对应在于空气质量的六个级别,指数越大,级别越高,说明污染越严重,对人体健康的影响也越明显.如图表1、2统计了北京市2016年元旦前后两周(2015-12-24至2016-01-06)实时空气污染指数和2015年6月3日11个监测点数据,两图表空气污染指数中位数之差的绝对值为82.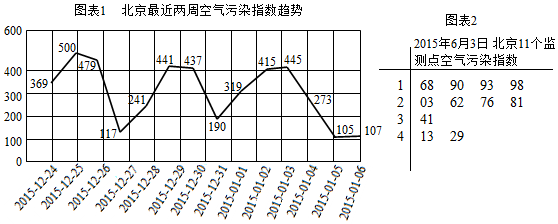
分析 根据中位数的定义,分别求出将图表1与图表2中的中位数,计算它们的差的绝对值即可.
解答 解:将图表1中所有数据从大到小排列为
105、107、117、190、241、273、319、369、
415、437、441、445、479、500,共14个数;
中间两数为319和369,
所以中位数为(319+369)÷2=344;
图表2共有11个数,中位数为262,
所以两图表中空气质量指数的中位数之差的绝对值为
|344-262|=82.
故答案为:82
点评 本题考查了中位数的定义与应用问题,也考查了识图与用图的能力,是基础题目.

练习册系列答案
相关题目
19.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F1作圆x2+y2=a2的切线,并延长交双曲线右支于点P,过右焦点F2作圆的切线交F1P于M,且M为F1P的中点,则双曲线的离心率e∈( )
| A. | (1,$\sqrt{2}$) | B. | ($\sqrt{2}$,$\sqrt{3}$) | C. | ($\sqrt{3},2$) | D. | (2,$\sqrt{5}$) |
16.设函数f(x)=-|x|,g(x)=lg(ax2-4x+1),若对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),则实数a的取值范围为( )
| A. | (-∞,4] | B. | (0,4] | C. | (-4,0] | D. | [4,+∞) |
3.平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为30°,$\overrightarrow{a}$=(1,0),|$\overrightarrow{b}$|=$\sqrt{3}$,则|$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | 2$\sqrt{3}$ | B. | 1 | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{2}}{2}$ |
13.若平面向量$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为2,且$\overrightarrow{b}$=(-1,3),则$\overrightarrow{a}$$•\overrightarrow{b}$=( )
| A. | $\sqrt{10}$ | B. | 10 | C. | 2$\sqrt{10}$ | D. | 20 |
20.已知函数f(x)=x3-3ax,若f(x)存在唯一的零点x0,则实数a的取值范围是( )
| A. | (0,+∞) | B. | [0,+∞) | C. | (-∞,0) | D. | (-∞,0] |
17.i是虚数单位,设复数z1=1+2i,z2=-3i,则z1•z1=( )
| A. | -6-3i | B. | 2-i | C. | 6-3i | D. | 6+3i |
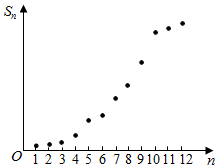 某市2015年前n个月空气质量优良的总天数Sn与n之间的关系如图所示.若前m月的月平均空气质量优良天数最大,则m值为( )
某市2015年前n个月空气质量优良的总天数Sn与n之间的关系如图所示.若前m月的月平均空气质量优良天数最大,则m值为( )